scRNAseq analysis part 2

Outline

HW2 will be posted by tomorrow morning.

Today, we are going to continue where we left off last Thursday. We will cover the following:

  • background information on example data

  • more on quality control

  • normalization

  • variable gene selection

  • principle component analysis

  • predicting cell cycle status

  • k-means clustering

  • hierarchical clustering

  • kNN

  • leiden clustering

Background

First, let’s start with a bit of background on the data that we have been using. In lecture 1, we talked about gastrulation:

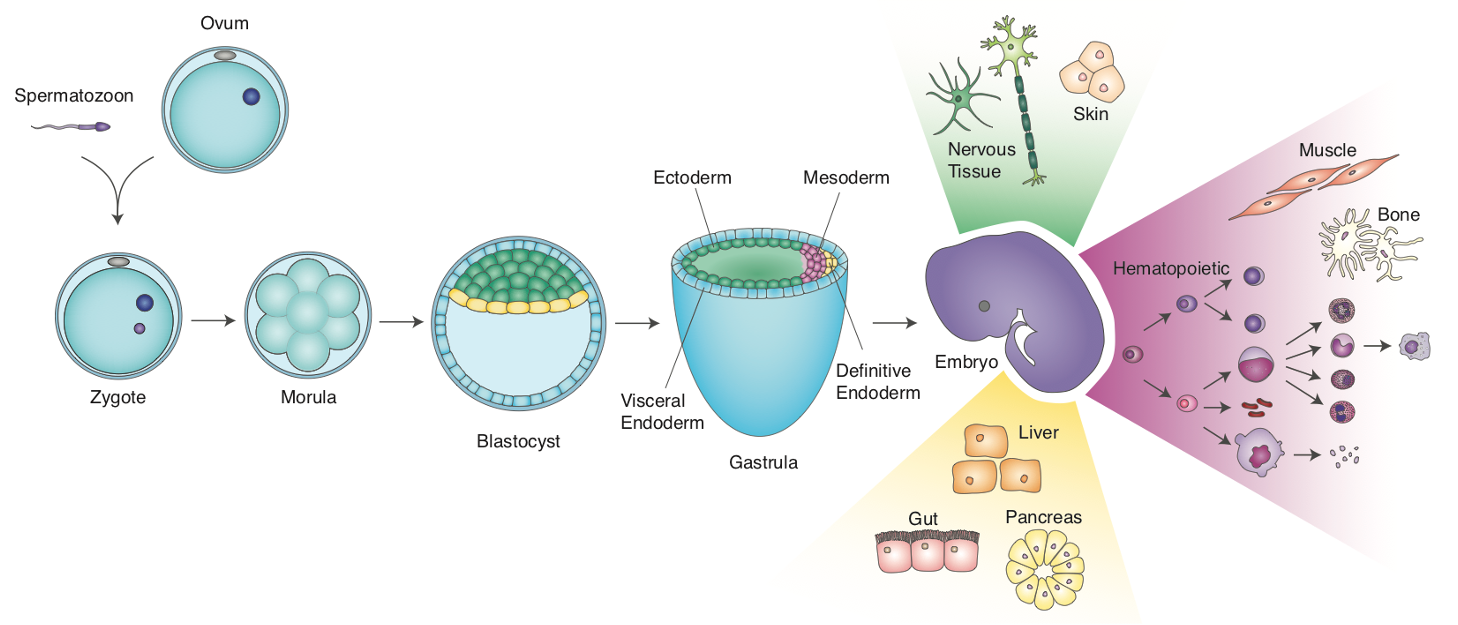
d7d571c1bb084360a87d2e52d74f39d0

Murine development. Figure credit: Emily KW Lo

When stem cell biologists differentiated pluripotent stem cells, they try to mimic aspects of this process. We have been curious as to the extent that that directed diff achieves this, so back in 2017/8 we turned to scRNAseq to define the cell types that emerge in the early stages of this in vitro process. We used the Embryoid Body method to allow differentiating mESCs to self-organize, along with Wnt/Activin induction of the primitive streak:

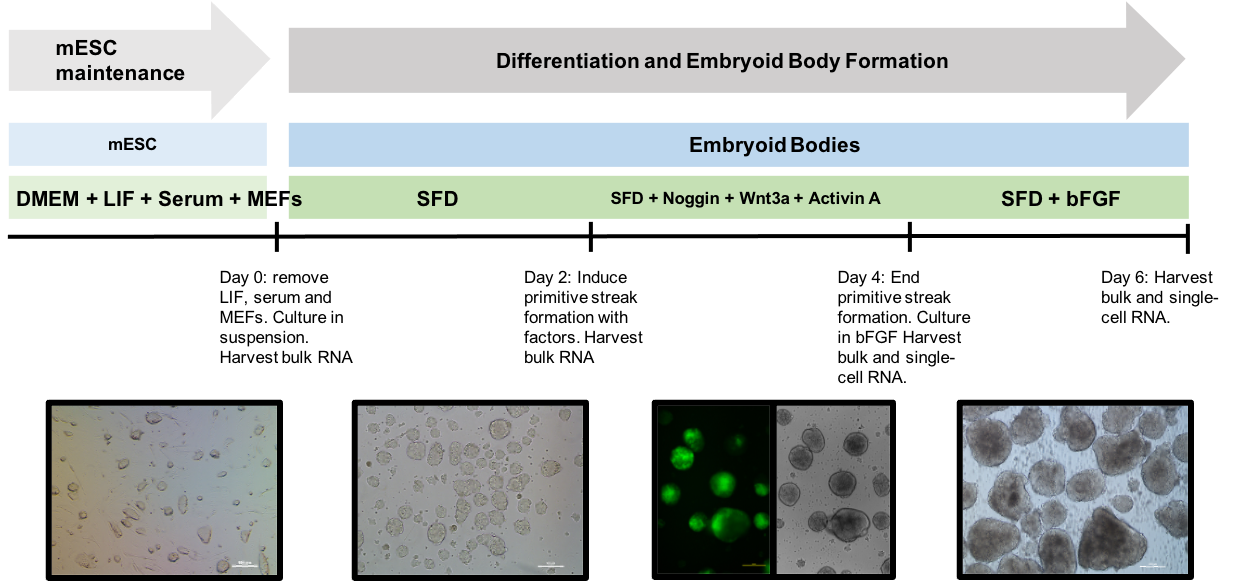
c10443fe1724478c817cf95fc1fec4b1

Embryoid body protocol. From Spangler et al, Stem Cell Research 2018

Note that the mESC line we used has a reported for T (a.k.a Brachyury), which allows us to monitor primitive streak induction.

At day 4, we sampled cells from this process and subjected them to single cell isolation and cDNA prep via the 10X Genomics Chromium instrument.

So the questions we want to address with this data are:

  • What cell types are present in these EBs at this stage?

  • What are the expression signatures of these cell types?

  • How do they compare to cells of the in vivo embryo? <- will address later

Re-load and initial QC

Let’s get the session started, and repeat the data loading, and qc metrics from last week

[ ]:

# If you have not already installed the following package, then please to so
# !pip3 install leidenalg

[2]:

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scanpy as sc
import scipy as sp
import numpy as np
import warnings
warnings.filterwarnings('ignore')
sc.settings.set_figure_params(dpi=80)

[ ]:

# adata = sc.read_10x_mtx("/Users/pcahan/Dropbox (Personal)/data/cscb/2022/d4/", var_names='gene_symbols',cache=True, gex_only=True)
# adata.obs['sampleName'] = "mEB_day4"
# adata.var['mt']= adata.var_names.str.startswith(("mt-"))
# adata.var['ribo'] = adata.var_names.str.startswith(("Rps","Rpl"))
# sc.pp.calculate_qc_metrics(adata, qc_vars=['ribo', 'mt'], percent_top=None, log1p=False, inplace=True)

Let’s save this as a h5ad file

[ ]:

# adata.write_h5ad("/Users/pcahan/Dropbox (Personal)/data/cscb/2022/d4/scb_2022_d4_raw.h5ad")
!pwd

[3]:

# adata = sc.read("/Users/patrickcahan/Dropbox (Personal)/data/cscb/2022/d4/cscb_2022_d4_raw.h5ad")
adata = sc.read("/Users/patrickcahan/Dropbox (Personal)/data/cscb/2022/d4/cscb_2022_d4_raw.h5ad")

adata.obs

[3]:
sampleName n_genes_by_counts total_counts total_counts_ribo pct_counts_ribo total_counts_mt pct_counts_mt
AAACATACCCTACC-1 mEB_day4 1212 2238.0 629.0 28.105453 28.0 1.251117
AAACATACGTCGTA-1 mEB_day4 1588 3831.0 1267.0 33.072304 34.0 0.887497
AAACATACTTTCAC-1 mEB_day4 1538 3381.0 961.0 28.423544 2.0 0.059154
AAACATTGCATTGG-1 mEB_day4 1221 2489.0 750.0 30.132584 24.0 0.964243
AAACATTGCTTGCC-1 mEB_day4 2661 9510.0 3132.0 32.933754 71.0 0.746583
... ... ... ... ... ... ... ...
TTTGACTGAGGCGA-1 mEB_day4 2446 6908.0 1999.0 28.937466 65.0 0.940938
TTTGACTGCATTGG-1 mEB_day4 2906 9558.0 3067.0 32.088303 91.0 0.952082
TTTGACTGCTGGAT-1 mEB_day4 1475 3280.0 1035.0 31.554878 22.0 0.670732
TTTGACTGGTGAGG-1 mEB_day4 2808 9123.0 2923.0 32.039898 55.0 0.602872
TTTGACTGTACAGC-1 mEB_day4 3518 14918.0 5091.0 34.126560 91.0 0.610001

5405 rows × 7 columns

Cell filtering

Recall the doublet problem. 10x has estimated the double rate for their 3’ products:

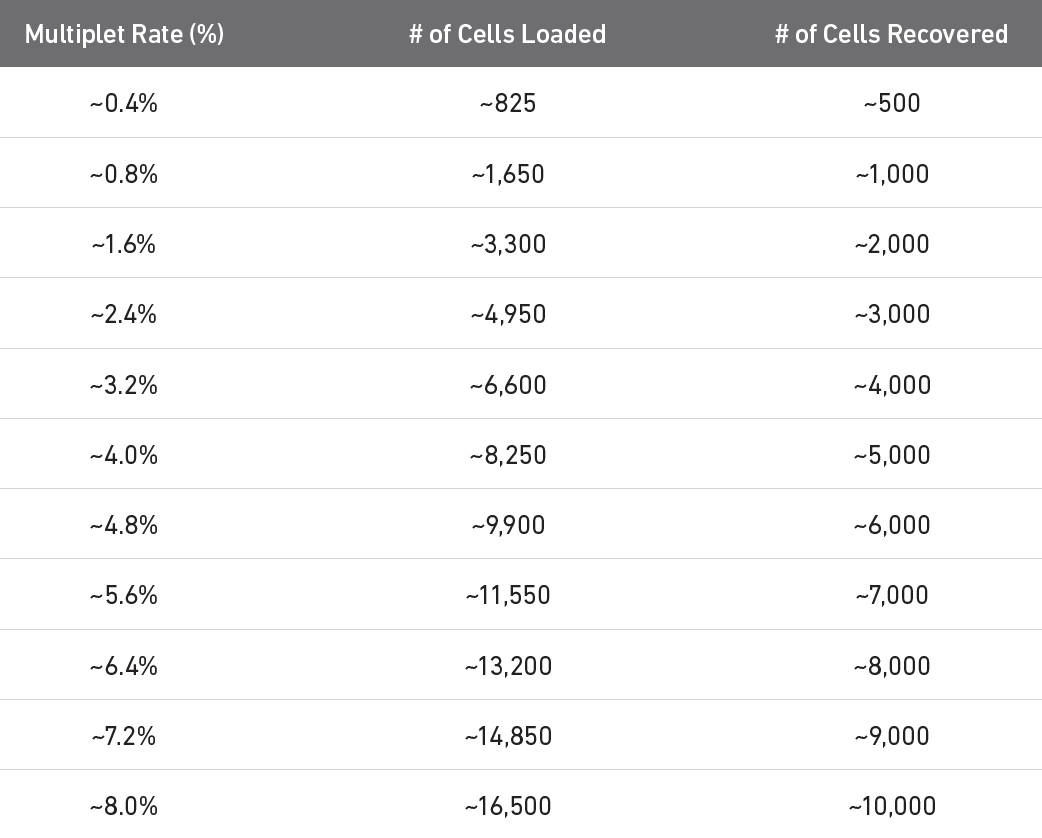
e67a714e74344e09bfdf806975be86c0

Multiplet table for 3’ v3.1 (see 10x website).

Let’s filter out cells based on the following: - the top 5% of cells based on total counts to exclude possible doublets - cells with < 500 genes based on n_genes_by_counts and - cells with > 10% pct_counts_mt - cells with < 50% ribosomal counts

[4]:

print("Number of cells: ",adata.n_obs)

# figure out the total counts == 95 percentile
thresh = np.percentile(adata.obs['total_counts'],95)
print("95th percentile: ",thresh)


Number of cells:  5405
95th percentile:  12928.400000000001

[5]:


adata = adata[adata.obs['total_counts'] < thresh, :]
print("Number of cells: ",adata.n_obs)

Number of cells:  5134

[6]:

# filter for % mt
adata = adata[adata.obs['pct_counts_mt'] < 10, :]
print("Number of cells: ",adata.n_obs)

Number of cells:  5133

[7]:


# filter for % ribo > 50%
adata = adata[adata.obs['pct_counts_ribo'] < 50, :]
print("Number of cells: ",adata.n_obs)

Number of cells:  5109

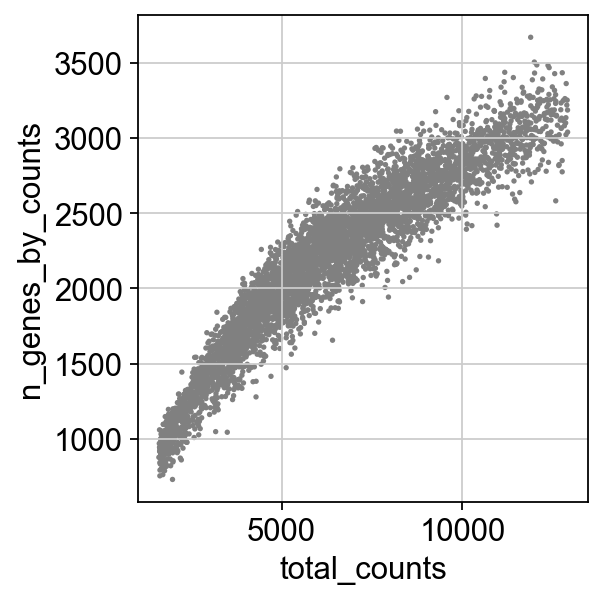
[8]:

sc.pl.scatter(adata, x='total_counts', y='n_genes_by_counts')
../_images/day_07_scRNAseq_analysis_part_2_14_0.png

Gene filtering

We also want to exclude genes that are only detected sporadically. In this case, let’s set this threshold to at least 5 cells:

[9]:

print("Number of genes: ",adata.n_vars)
gThresh = 5

sc.pp.filter_genes(adata, min_cells=gThresh)
print("Number of genes: ",adata.n_vars)

Number of genes:  27998

Trying to set attribute `.var` of view, copying.

Number of genes:  15677

I also advocate excluding genes that are highly expressed but that are not informative. For example, the ribosomal genes, and Malat1. Public service announcement/correction on Ribo genes

[10]:

sc.pl.highest_expr_genes(adata, n_top=50,palette="Blues", width=.3)
../_images/day_07_scRNAseq_analysis_part_2_18_0.png 
[12]:

mito_genes = adata.var_names.str.startswith('mt-')
ribo_genes = adata.var_names.str.startswith(("Rpl","Rps"))
malat_gene = adata.var_names.str.startswith("Malat1")

[13]:

mito_genes

[13]:

array([False, False, False, ..., False, False, False])

[14]:

remove = np.add(mito_genes, ribo_genes)
remove = np.add(remove, malat_gene)

[15]:

np.add([True, True], [False, True])

[15]:

array([ True,  True])

[19]:

keep = np.invert(remove)
keep

[19]:

array([ True,  True,  True, ...,  True,  True,  True])

[17]:

print(len(keep) - np.count_nonzero(keep))

120

[18]:

adata = adata[:,keep].copy()
print("Number of genes: ",adata.n_vars)

Number of genes:  15557

Normalization

First, do a a total count normalization such that each barcode/cell ends up with the same total expression. It is also common practice to log the resulting values. BUT, lets keep a copy of the raw counts in a .raw slot:

[21]:

adata.raw = adata
sc.pp.normalize_total(adata, target_sum=1e4)
sc.pp.log1p(adata)

Highly variable genes

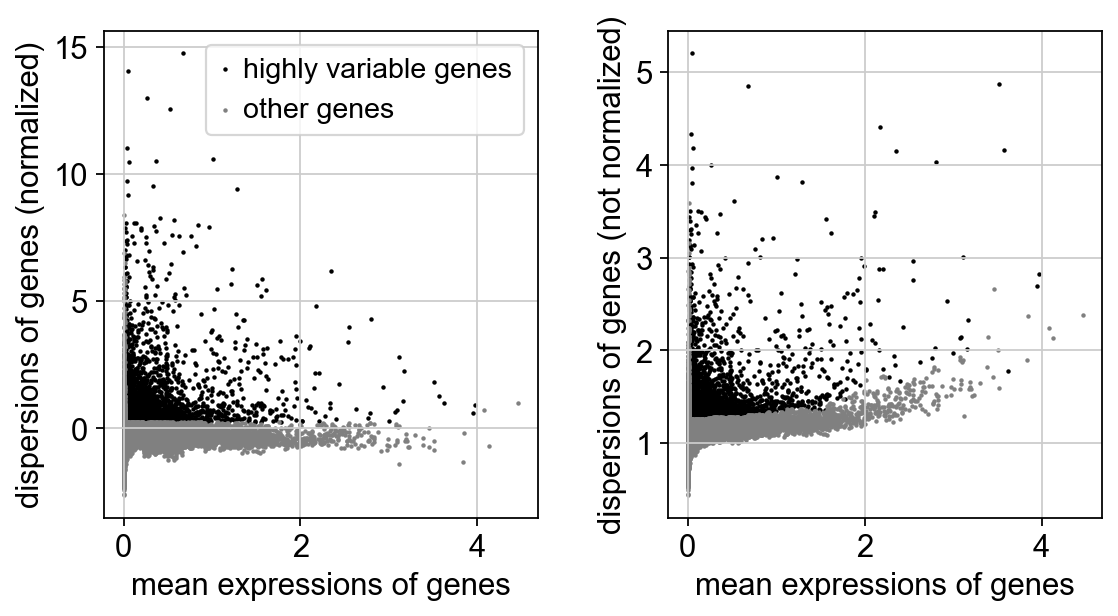
Common practice to limit some parts of analysis to those variables/genes that exhibit some degree of variation in their values across the data. We call these highly variable genes, or HVG for short. To find these, calculate some gene statistics, which when combined with thresholds below, determine which genes are considered HVG. These metrics are mean expression and dispersion (variance / mean). Variance is defined as the expected squared deviation of gene expression. The normalized dispersion is calculated by scaling based on a bin of mean expression.

[22]:

sc.pp.highly_variable_genes(adata, min_mean=0.0125, max_mean=4, min_disp=0.25)
adata.var

[22]:
gene_ids mt ribo n_cells_by_counts mean_counts pct_dropout_by_counts total_counts n_cells highly_variable means dispersions dispersions_norm
Xkr4 ENSMUSG00000051951 False False 37 0.007031 99.315449 38.0 36 False 0.016160 0.963224 -0.793932
Sox17 ENSMUSG00000025902 False False 214 0.121369 96.040703 656.0 200 True 0.245262 2.410920 5.548414
Mrpl15 ENSMUSG00000033845 False False 3083 1.093617 42.960222 5911.0 2812 False 1.177424 1.363713 0.200615
Lypla1 ENSMUSG00000025903 False False 1300 0.289732 75.948196 1566.0 1177 False 0.522485 1.201372 -0.183017
Tcea1 ENSMUSG00000033813 False False 2025 0.507678 62.534690 2744.0 1853 False 0.782621 1.229463 -0.082616
... ... ... ... ... ... ... ... ... ... ... ... ...
Vamp7 ENSMUSG00000051412 False False 810 0.168178 85.013876 909.0 729 True 0.342715 1.299276 0.339964
Spry3 ENSMUSG00000061654 False False 5 0.000925 99.907493 5.0 5 False 0.002576 1.157724 -0.113710
PISD ENSMUSG00000095041 False False 2648 0.801295 51.008326 4331.0 2480 True 1.128138 1.547616 0.890088
DHRSX ENSMUSG00000063897 False False 363 0.071230 93.283996 385.0 331 False 0.147803 1.127410 -0.219726
CAAA01147332.1 ENSMUSG00000095742 False False 13 0.002405 99.759482 13.0 10 False 0.006262 1.560301 1.294218

15557 rows × 12 columns

[23]:

sc.pl.highly_variable_genes(adata)
../_images/day_07_scRNAseq_analysis_part_2_30_0.png

Gene scaling

Often, we are more interested in changes in gene expression rather than absolute expression levels, and how these changes in expression contribute to variation in cell state or cell type. To focus on this aspect of expression, we will transform expression values using the z-score, which just adjust the expression of each gene by subtracting the mean, and then dividing by the standard deviation. This is also helpful for the PCA that is performed below.

[24]:

sc.pp.scale(adata, max_value=10)

Principal components analysis

There are two facts that make PCA a good tool of analzying scRNAseq data. First, genes are expressed in coordinated fashion, meaning that many have correlated expression patterns. Second scRNAseq data is noisy.

PCA allows us to reduce a high dimensional data set into a lower dimension in which much of the total variation is maintained. To understand PCA, you need to know linear algebra. In essence, it identifies sets of linear combinations of genes in such a way that they uncorrelated and explain most variation in the data. The function call does the following

  • compute the covariance matrix (correlation between each pair of genes)

  • finding eigenvectors (directions of axes that maximize that variance), orthogonal to each other

Later, we might want to select npcs = the number of pcs that will be used for downstream clustering.

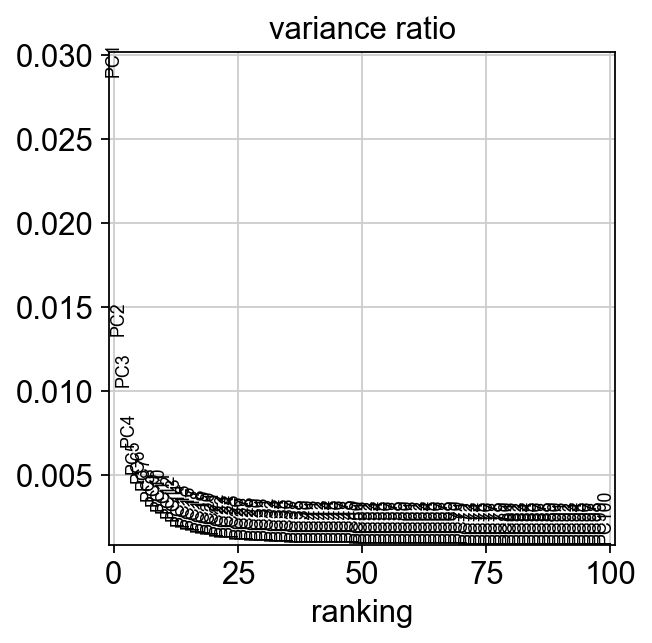
[25]:

sc.tl.pca(adata, n_comps=100)
sc.pl.pca_variance_ratio(adata,100, )
../_images/day_07_scRNAseq_analysis_part_2_34_0.png 
[26]:

sc.set_figure_params(figsize="10, 4")
sc.pl.pca_variance_ratio(adata,100, )
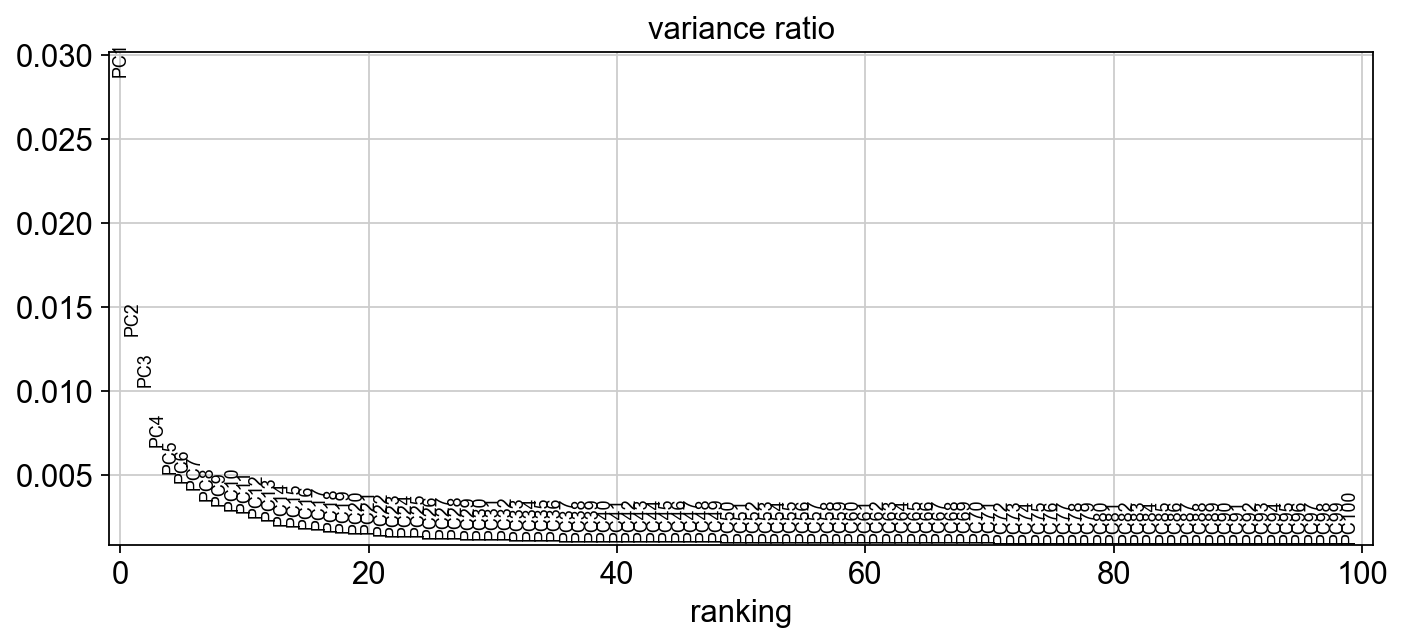
../_images/day_07_scRNAseq_analysis_part_2_35_0.png 
[27]:

np.shape(adata.obsm["X_pca"])

[27]:

(5109, 100)

[28]:

np.shape(adata.varm["PCs"])

[28]:

(15557, 100)

Now, let’s just take a look at how the data look! Plot the cells based on the PCs.

[29]:

# sc.set_figure_params(figsize="5, 5")
fig, axs = plt.subplots(2,2, figsize=(5,5), constrained_layout=True)
sc.pl.pca_scatter(adata, ax=axs[0,0], show=False, size=10)
sc.pl.pca_scatter(adata, components="1,3", ax=axs[0,1], show=False, size=10)
sc.pl.pca_scatter(adata, components="2,3", ax=axs[1,0], show=False, size=10)
sc.pl.pca_scatter(adata, components="1,4", ax=axs[1,1], show=False, size=10)

[29]:

<AxesSubplot:xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_39_1.png

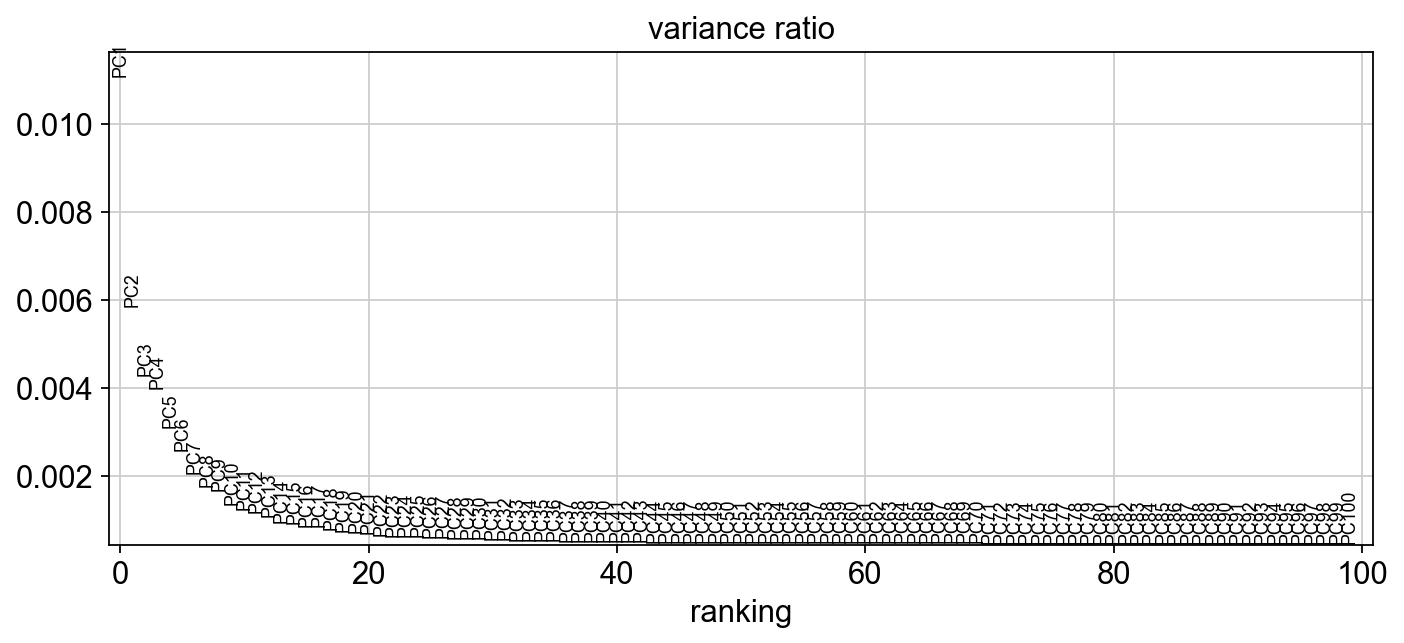
What happens if you don’t use HVG in PCA?

[30]:

sc.tl.pca(adata, n_comps=100, use_highly_variable=False)
sc.set_figure_params(figsize="10, 4")
sc.pl.pca_variance_ratio(adata,100, )
../_images/day_07_scRNAseq_analysis_part_2_41_0.png 
[31]:

fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="Zfp42", ax=axs[0,0], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="1,3", ax=axs[0,1], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="2,3", ax=axs[1,0], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="1,4", ax=axs[1,1], show=False, size=10, use_raw=False)

[31]:

<AxesSubplot:title={'center':'Zfp42'}, xlabel='PC1', ylabel='PC4'>
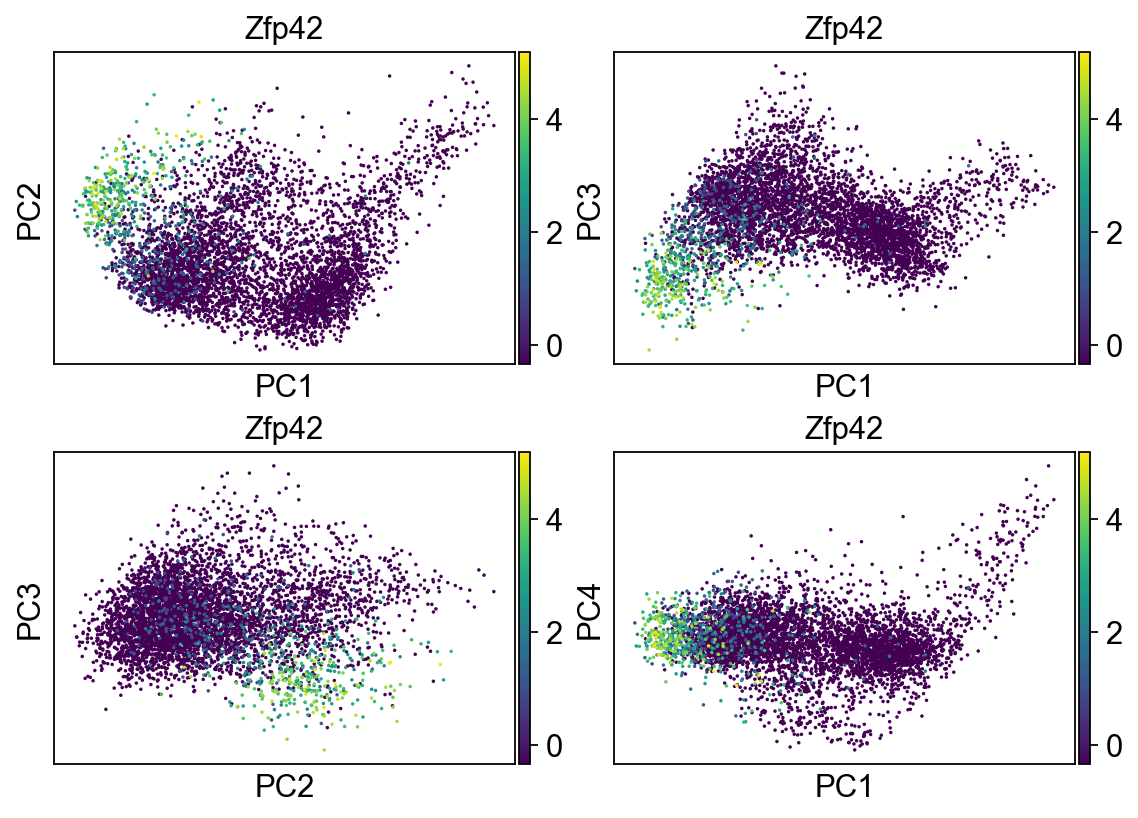
../_images/day_07_scRNAseq_analysis_part_2_42_1.png

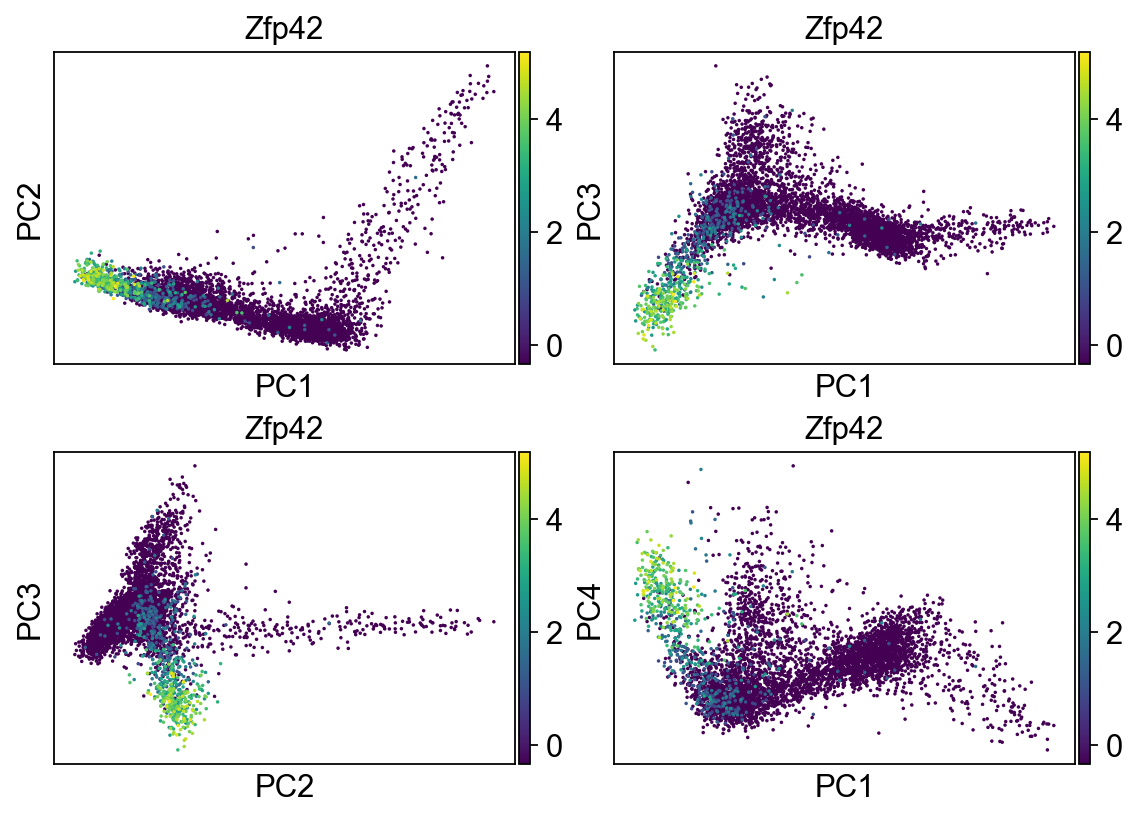
Let’s go back to use the HVG

[32]:

sc.tl.pca(adata, n_comps=100, use_highly_variable=True)

[33]:

fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="Zfp42", ax=axs[0,0], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="1,3", ax=axs[0,1], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="2,3", ax=axs[1,0], show=False, size=10, use_raw=False)
sc.pl.pca_scatter(adata, color="Zfp42", components="1,4", ax=axs[1,1], show=False, size=10, use_raw=False)

[33]:

<AxesSubplot:title={'center':'Zfp42'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_45_1.png

Cell cycle status

Recall in Lecture 5 when we covered Drop-Seq, how the authors were able to predict phase of cell cycle. What is cell cycle?

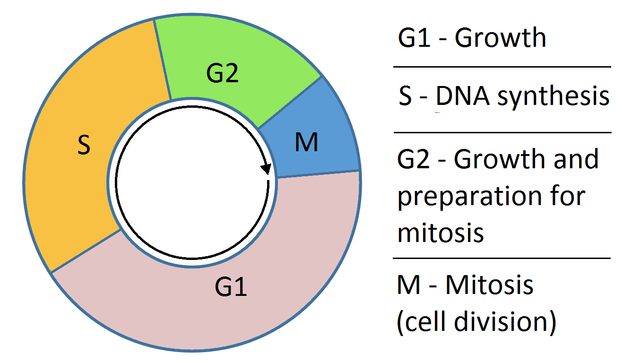
97651ab662c54c3fba5e3d9ba42d6f30

Cell cycle. Credit: Wikipedia.

This was done by summarizing the expression of genes associated with distinct phases of cell cycle and normalizing this value to a background value. Let’s perform a similar analysis here. First, please fetch the table of mouse genes:

[ ]:

# !wget https://compstemcellbio.s3.amazonaws.com/2022/resources/mouseCellCycle_050218.csv

[34]:

#cell_cycle_genes = [x.strip() for x in open("/Users/pcahan/Dropbox (Personal)/data/cscb/2022/resources/mouseCellCycle_050218.csv")]
cell_cycle_genes = [x.strip() for x in open("/Users/patrickcahan/Dropbox (Personal)/data/cscb/2022/resources/mouseCellCycle_050218.csv")]

[35]:


print("n cc genes:", len(cell_cycle_genes))
cell_cycle_genes[0:5]

n cc genes: 114

[35]:

['Mcm5', 'Pcna', 'Tyms', 'Fen1', 'Mcm2']

Split into genes associated with S phase, and those associated with G2M

[36]:

s_genes = cell_cycle_genes[:43]
g2m_genes = cell_cycle_genes[43:]

# now intersect these with genes present in the annData object
cell_cycle_genes = [x for x in cell_cycle_genes if x in adata.var_names]
print("n cc genes:", len(cell_cycle_genes))

n cc genes: 111

[37]:


s_genes = [x for x in s_genes if x in adata.var_names]
g2m_genes = [x for x in g2m_genes if x in adata.var_names]

[38]:

sc.tl.score_genes_cell_cycle(adata, s_genes=s_genes, g2m_genes=g2m_genes)

[39]:

adata.obs

[39]:
sampleName n_genes_by_counts total_counts total_counts_ribo pct_counts_ribo total_counts_mt pct_counts_mt S_score G2M_score phase
AAACATACCCTACC-1 mEB_day4 1212 2238.0 629.0 28.105453 28.0 1.251117 -0.025818 0.066043 G2M
AAACATACGTCGTA-1 mEB_day4 1588 3831.0 1267.0 33.072304 34.0 0.887497 0.193831 0.545027 G2M
AAACATACTTTCAC-1 mEB_day4 1538 3381.0 961.0 28.423544 2.0 0.059154 0.453981 0.562032 G2M
AAACATTGCATTGG-1 mEB_day4 1221 2489.0 750.0 30.132584 24.0 0.964243 0.001577 0.840160 G2M
AAACATTGCTTGCC-1 mEB_day4 2661 9510.0 3132.0 32.933754 71.0 0.746583 0.446344 0.671123 G2M
... ... ... ... ... ... ... ... ... ... ...
TTTGACTGACTCTT-1 mEB_day4 2941 11419.0 4406.0 38.584812 44.0 0.385323 -0.164811 0.345561 G2M
TTTGACTGAGGCGA-1 mEB_day4 2446 6908.0 1999.0 28.937466 65.0 0.940938 0.704966 0.669519 S
TTTGACTGCATTGG-1 mEB_day4 2906 9558.0 3067.0 32.088303 91.0 0.952082 1.178114 0.898342 S
TTTGACTGCTGGAT-1 mEB_day4 1475 3280.0 1035.0 31.554878 22.0 0.670732 0.246748 0.693743 G2M
TTTGACTGGTGAGG-1 mEB_day4 2808 9123.0 2923.0 32.039898 55.0 0.602872 -0.162199 1.935829 G2M

5109 rows × 10 columns

[40]:

adata_cc_genes = adata[:, cell_cycle_genes].copy()
sc.pp.pca(adata_cc_genes,use_highly_variable=False)

[41]:

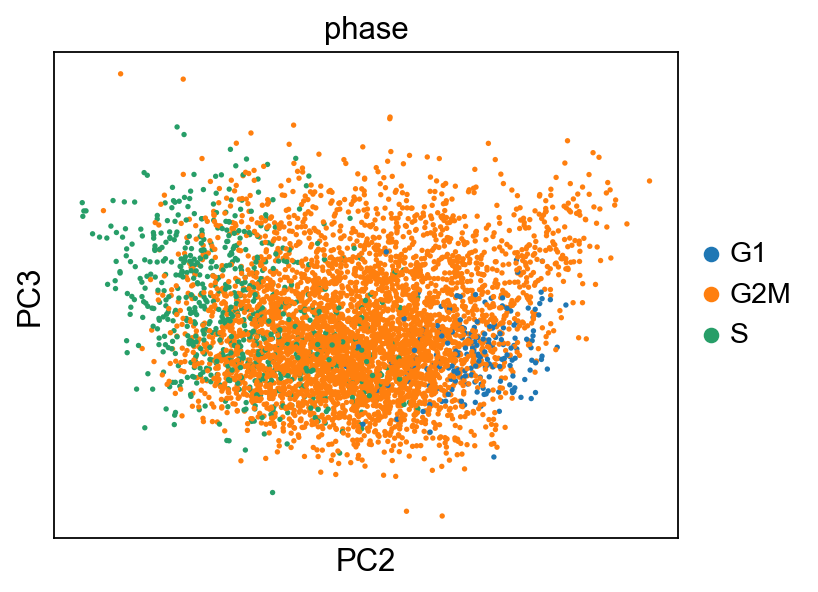
sc.set_figure_params(figsize="5, 4")
sc.pl.pca_scatter(adata_cc_genes, color=["phase"], components="2,3")

... storing 'phase' as categorical
../_images/day_07_scRNAseq_analysis_part_2_56_1.png 
[42]:

sc.pl.pca_scatter(adata_cc_genes, color=("Mcm5", "Pcna", "Cdk1", "Top2a"), components="2,3", use_raw=False)
../_images/day_07_scRNAseq_analysis_part_2_57_0.png 
[43]:

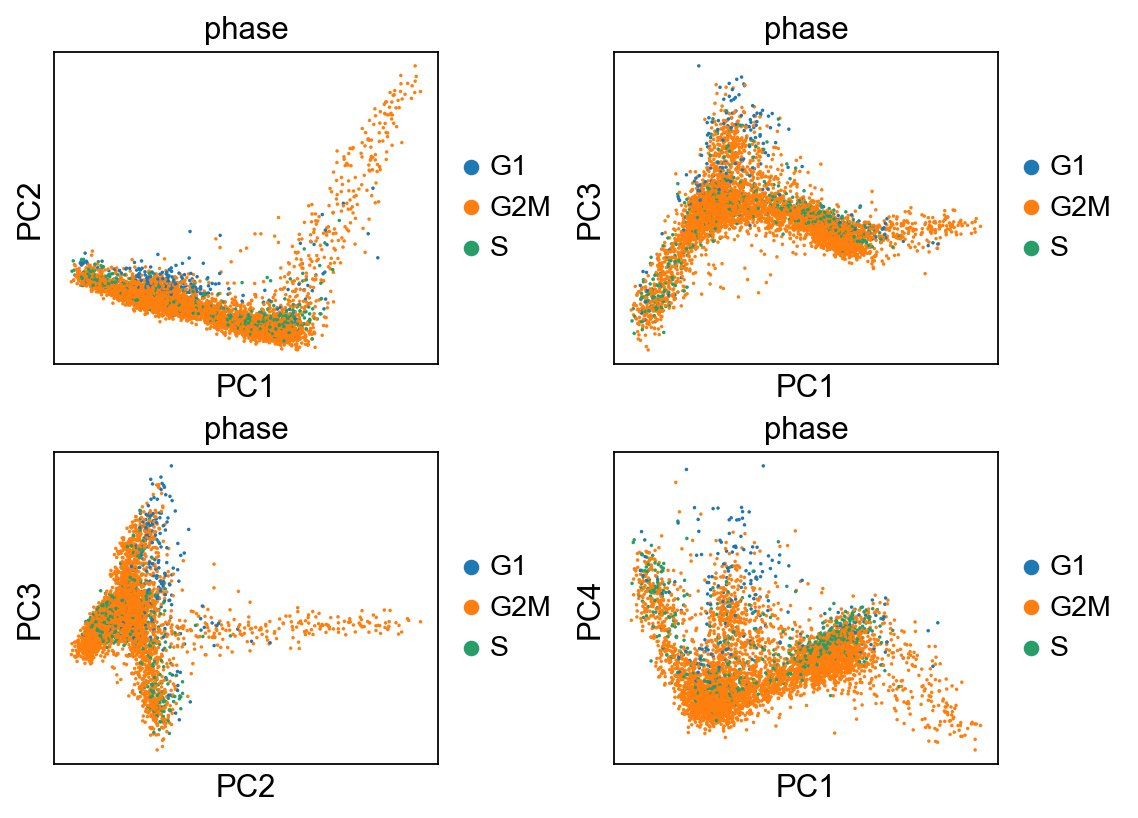
fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="phase", ax=axs[0,0], show=False, size=10)
sc.pl.pca_scatter(adata, color="phase", components="1,3", ax=axs[0,1], show=False, size=10)
sc.pl.pca_scatter(adata, color="phase", components="2,3", ax=axs[1,0], show=False, size=10)
sc.pl.pca_scatter(adata, color="phase", components="1,4", ax=axs[1,1], show=False, size=10)

... storing 'phase' as categorical

[43]:

<AxesSubplot:title={'center':'phase'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_58_2.png 
[44]:

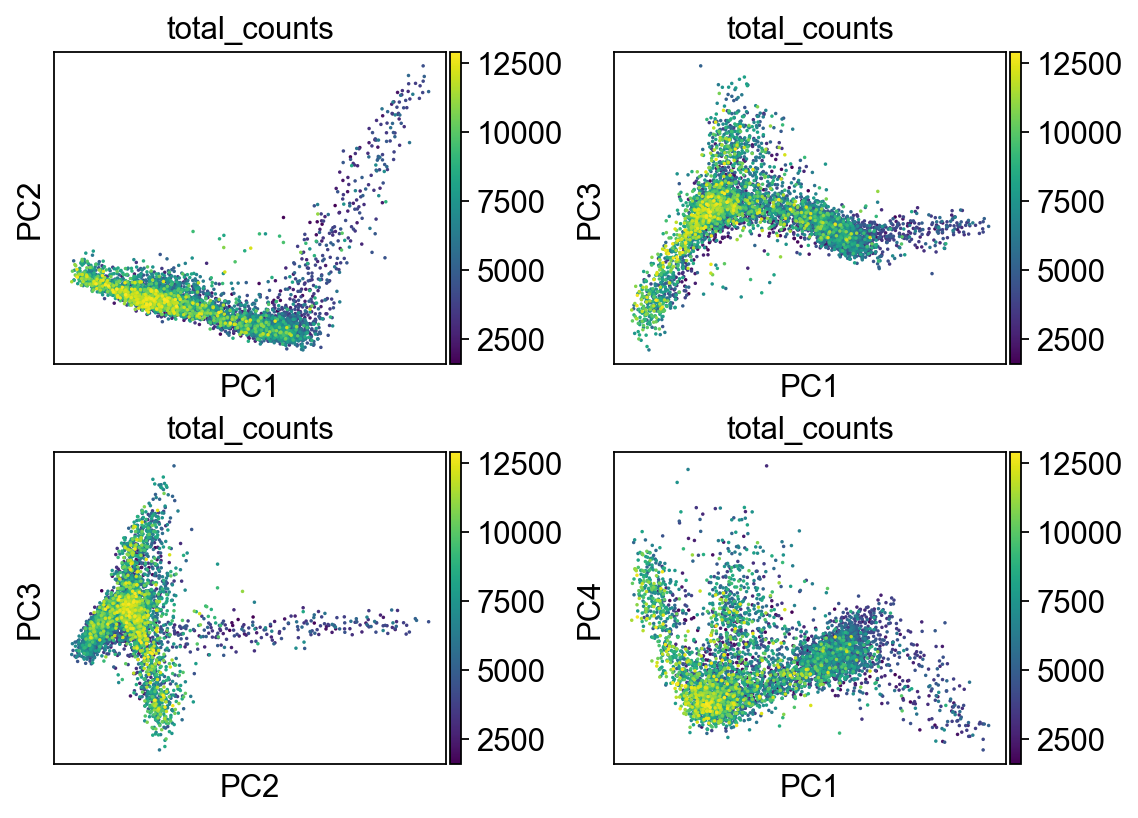
fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="total_counts", ax=axs[0,0], show=False, size=10)
sc.pl.pca_scatter(adata, color="total_counts", components="1,3", ax=axs[0,1], show=False, size=10)
sc.pl.pca_scatter(adata, color="total_counts", components="2,3", ax=axs[1,0], show=False, size=10)
sc.pl.pca_scatter(adata, color="total_counts", components="1,4", ax=axs[1,1], show=False, size=10)

[44]:

<AxesSubplot:title={'center':'total_counts'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_59_1.png

Clustering

Let’s start with one of the simplest clustering methods: k-means. It is an iterative process that starts with k randomly sampled points. It assigns cells to cluster defined by the nearest point. Then, it updates the points as the center of the newly defined cluster, repeating this process unitl convergence or a specified number of times. The key concept here is that of the distance metric, which quantifies how close cells are. Eucliean distance is commonly used, as are different transformations of correlation measures (e.g. 1 - PCC).

[45]:

from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score

[46]:

kmeans = KMeans(n_clusters=2, random_state=0).fit(adata.obsm["X_pca"])
adata.obs['kmeans2'] = kmeans.labels_.astype(str)

[47]:

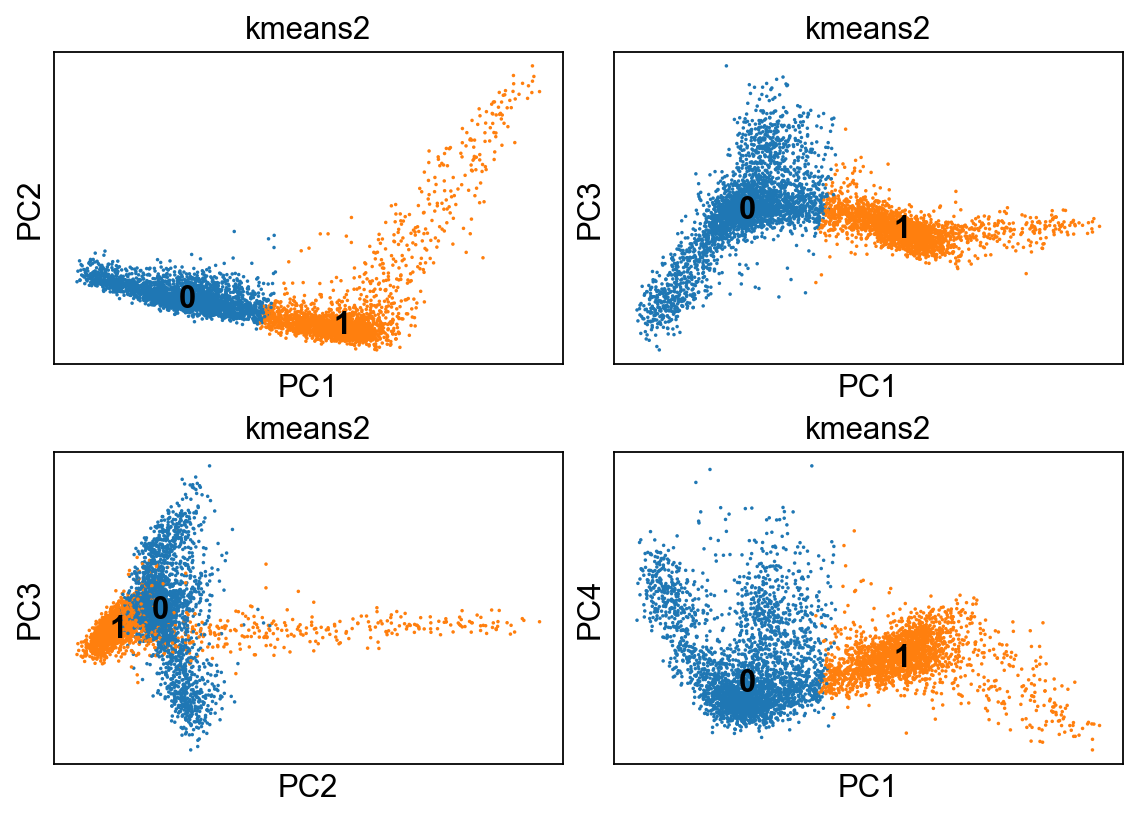
fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="kmeans2", ax=axs[0,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans2", components="1,3", ax=axs[0,1], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans2", components="2,3", ax=axs[1,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans2", components="1,4", ax=axs[1,1], show=False, size=10, use_raw=False, legend_loc="on data")

... storing 'kmeans2' as categorical

[47]:

<AxesSubplot:title={'center':'kmeans2'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_63_2.png 
[48]:

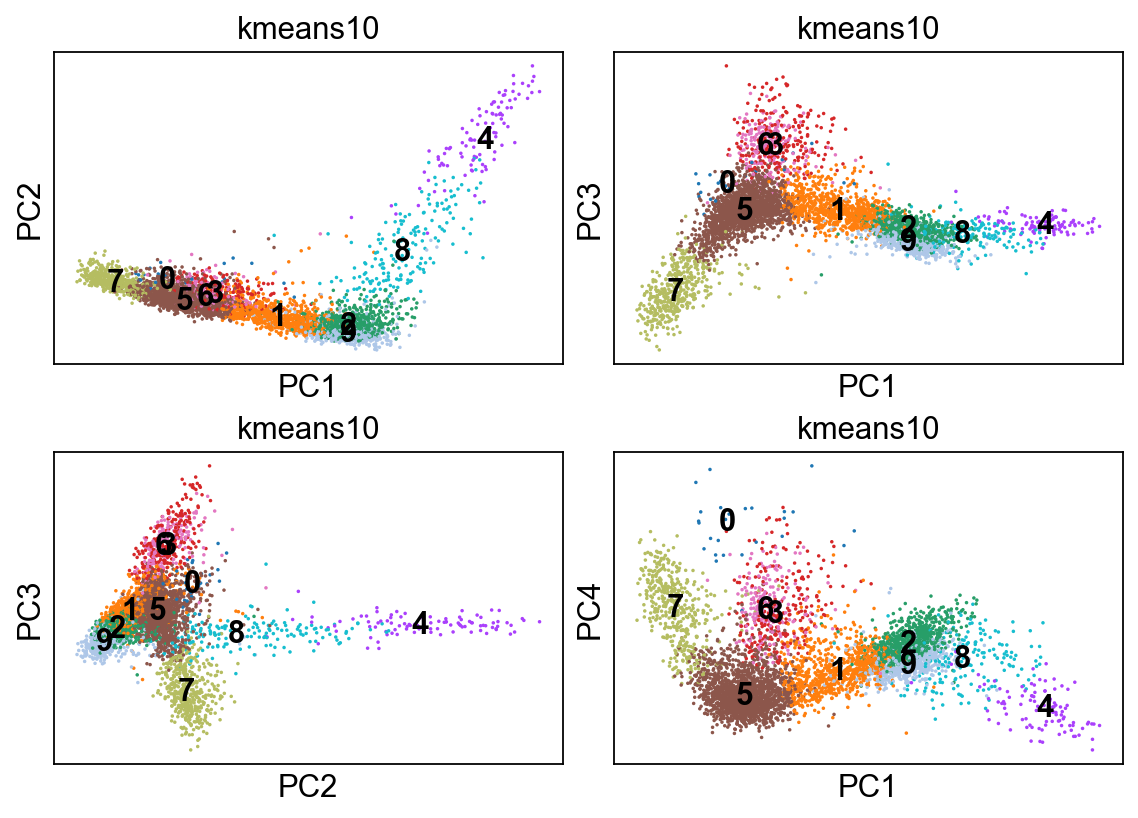
kmeans = KMeans(n_clusters=10, random_state=0).fit(adata.obsm["X_pca"])
adata.obs['kmeans10'] = kmeans.labels_.astype(str)

fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="kmeans10", ax=axs[0,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans10", components="1,3", ax=axs[0,1], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans10", components="2,3", ax=axs[1,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans10", components="1,4", ax=axs[1,1], show=False, size=10, use_raw=False, legend_loc="on data")

... storing 'kmeans10' as categorical

[48]:

<AxesSubplot:title={'center':'kmeans10'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_64_2.png 
[49]:

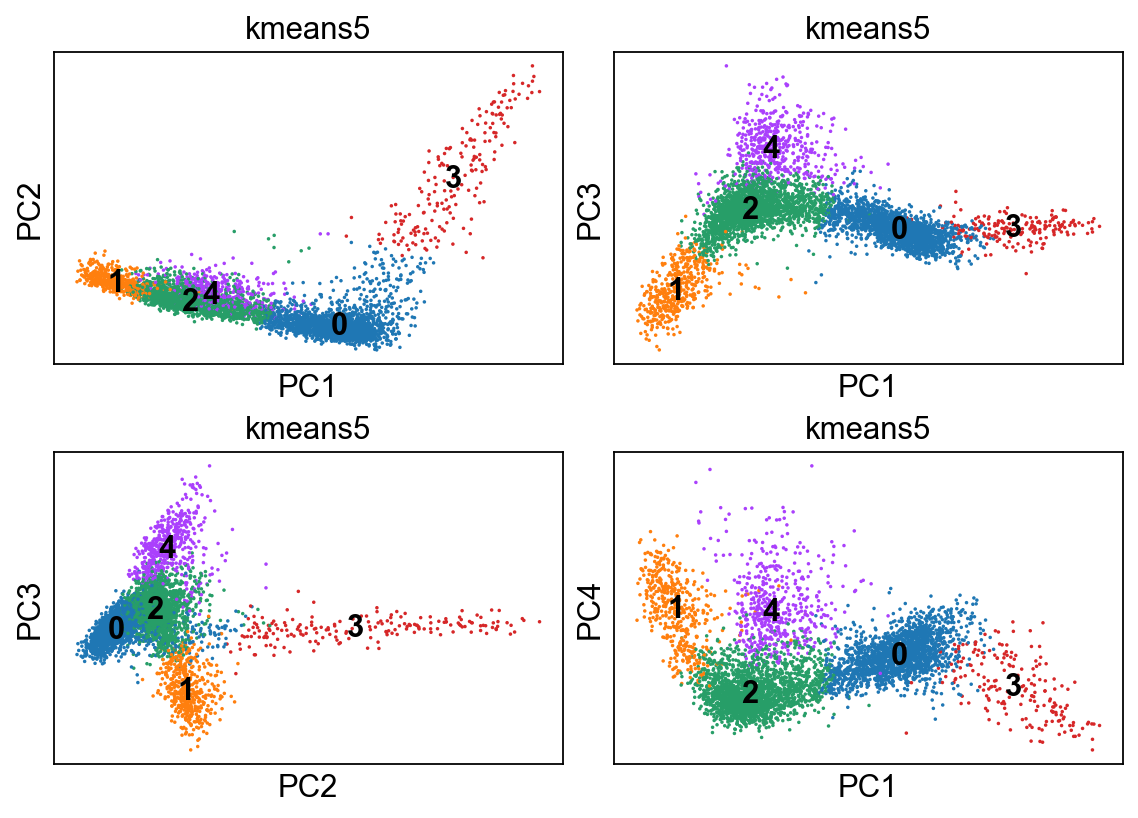
kmeans = KMeans(n_clusters=5, random_state=0).fit(adata.obsm["X_pca"])
adata.obs['kmeans5'] = kmeans.labels_.astype(str)

[50]:


fig, axs = plt.subplots(2,2, figsize=(7,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="kmeans5", ax=axs[0,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans5", components="1,3", ax=axs[0,1], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans5", components="2,3", ax=axs[1,0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="kmeans5", components="1,4", ax=axs[1,1], show=False, size=10, use_raw=False, legend_loc="on data")

... storing 'kmeans5' as categorical

[50]:

<AxesSubplot:title={'center':'kmeans5'}, xlabel='PC1', ylabel='PC4'>
../_images/day_07_scRNAseq_analysis_part_2_66_2.png

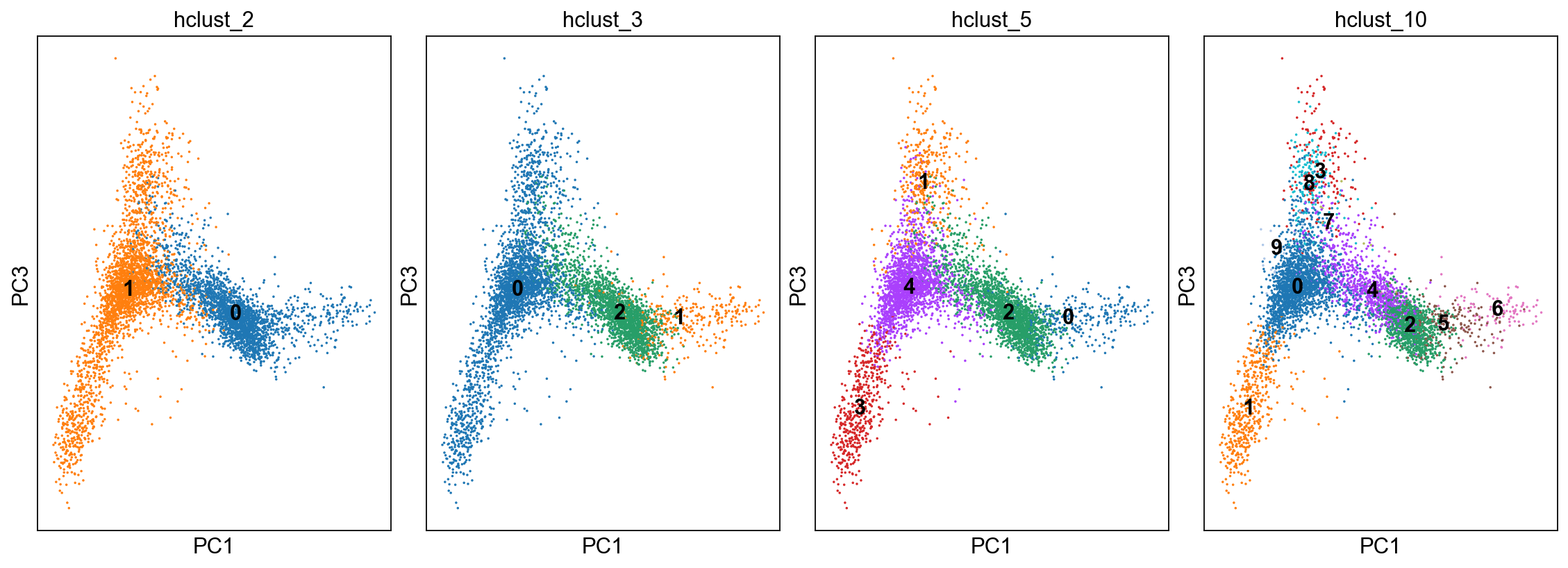
Now let’s try another simple method: hierarchical clustering. describe this method

[51]:

from sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
adata.obs['hclust_2'] = cluster.fit_predict(adata.obsm["X_pca"]).astype(str)

cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
adata.obs['hclust_3'] = cluster.fit_predict(adata.obsm["X_pca"]).astype(str)

cluster = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
adata.obs['hclust_5'] = cluster.fit_predict(adata.obsm["X_pca"]).astype(str)

cluster = AgglomerativeClustering(n_clusters=10, affinity='euclidean', linkage='ward')
adata.obs['hclust_10'] = cluster.fit_predict(adata.obsm["X_pca"]).astype(str)


[52]:

fig, axs = plt.subplots(1,4, figsize=(14,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="hclust_2", components="1,3",ax=axs[0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="hclust_3", components="1,3",ax=axs[1], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="hclust_5", components="1,3",ax=axs[2], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="hclust_10", components="1,3",ax=axs[3], show=False, size=10, use_raw=False, legend_loc="on data")

... storing 'hclust_2' as categorical
... storing 'hclust_3' as categorical
... storing 'hclust_5' as categorical
... storing 'hclust_10' as categorical

[52]:

<AxesSubplot:title={'center':'hclust_10'}, xlabel='PC1', ylabel='PC3'>
../_images/day_07_scRNAseq_analysis_part_2_69_2.png

One final class of clustering methods is based on deriving the k-nearest neighbor graph. Walk them through the concept, explain how used to transform adjacency matrix

a6357ca18b7b496796223056fd6f9d23

K-nearest neighbor graph. Credit: Wikipedia.

Recall the elbow plot. From this, we can pick out a reasonable n_pcs

[53]:

n_pcs = 20
n_neighbors = 15
sc.pp.neighbors(adata, n_neighbors=n_neighbors, n_pcs=n_pcs)

OMP: Info #271: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.

[54]:

sc.tl.leiden(adata, .25)



[ ]:

fig, axs = plt.subplots(1,3, figsize=(14,5), constrained_layout=True)
sc.pl.pca_scatter(adata, color="kmeans5", components="1,3",ax=axs[0], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="hclust_5", components="1,3",ax=axs[1], show=False, size=10, use_raw=False, legend_loc="on data")
sc.pl.pca_scatter(adata, color="leiden", components="1,3",ax=axs[2], show=False, size=10, use_raw=False, legend_loc="on data")

<AxesSubplot:title={'center':'leiden'}, xlabel='PC1', ylabel='PC3'>
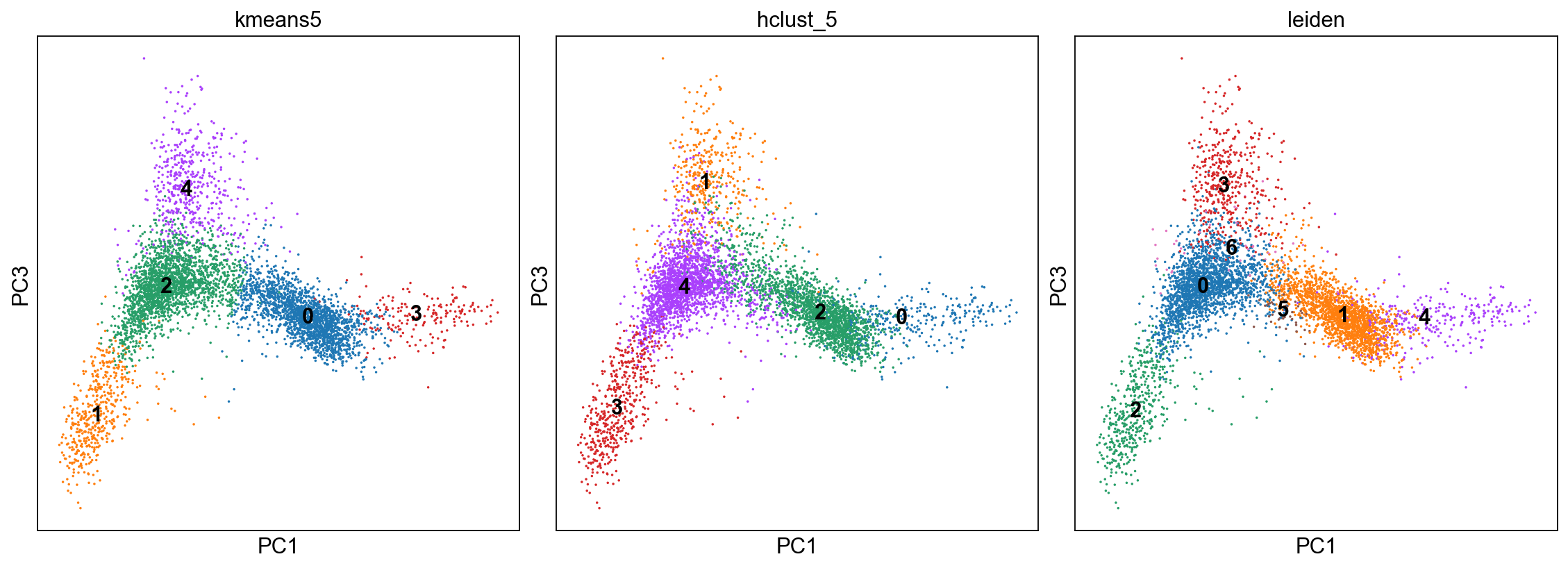
../_images/day_07_scRNAseq_analysis_part_2_73_1.png

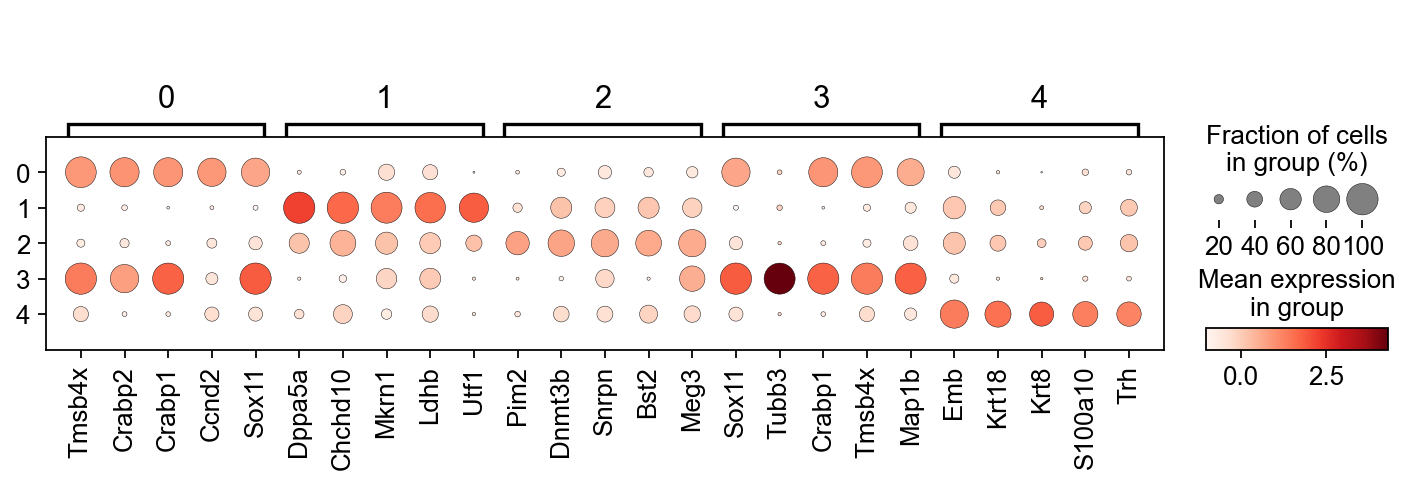
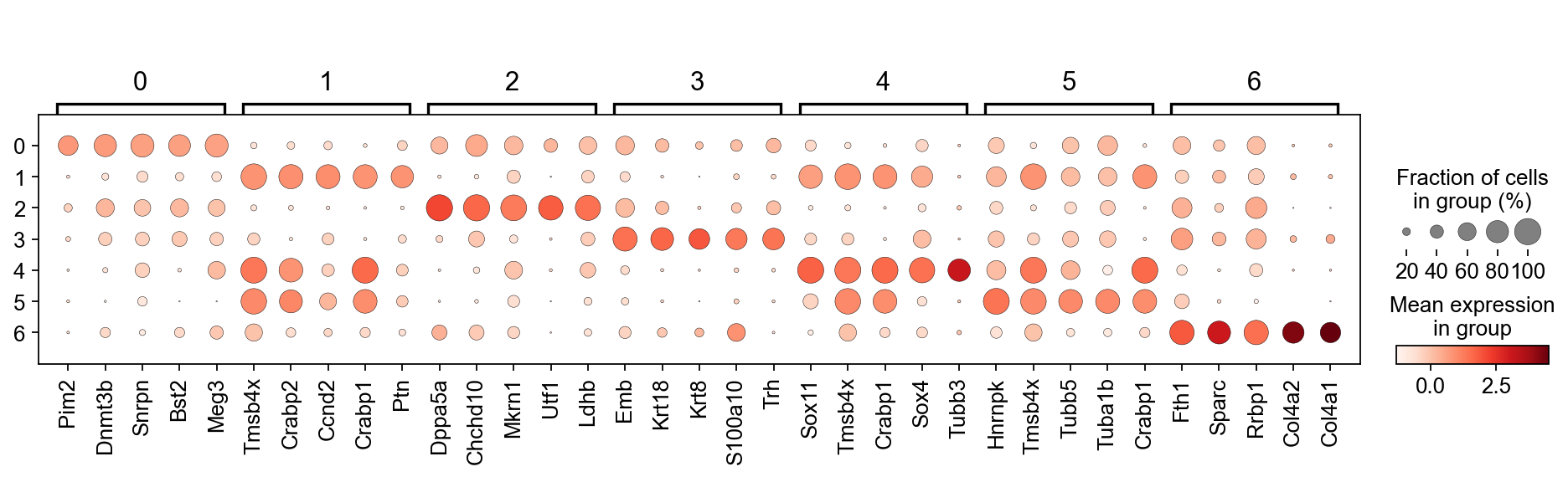
We only got to this point in the class. Below are two lines of code that 1.) perform a t-test to identify differentially expressed genes between clusters. It does this in by comparing mean expression of genes in each cluster vs all other clusters. 2.) ranking the genes according to their differential expression per cluster, and producing a dot plot of the top 5 genes per cluster.

[56]:

sc.tl.rank_genes_groups(adata,'leiden', use_raw=False)
sc.pl.rank_genes_groups_dotplot(adata, n_genes=5, groupby='leiden', use_raw=False, dendrogram=False)

WARNING: Default of the method has been changed to 't-test' from 't-test_overestim_var'
../_images/day_07_scRNAseq_analysis_part_2_75_1.png 
[57]:

sc.tl.rank_genes_groups(adata,'kmeans5', use_raw=False)
sc.pl.rank_genes_groups_dotplot(adata, n_genes=5, groupby='kmeans5', use_raw=False, dendrogram=False)

WARNING: Default of the method has been changed to 't-test' from 't-test_overestim_var'
../_images/day_07_scRNAseq_analysis_part_2_76_1.png