Lineage Tracing Analysis

Today, we will analyze sc lineage tracing data with CoSpar Wang et al 2022

Much of the tutorial today comes straight from CoSpar’s documentation

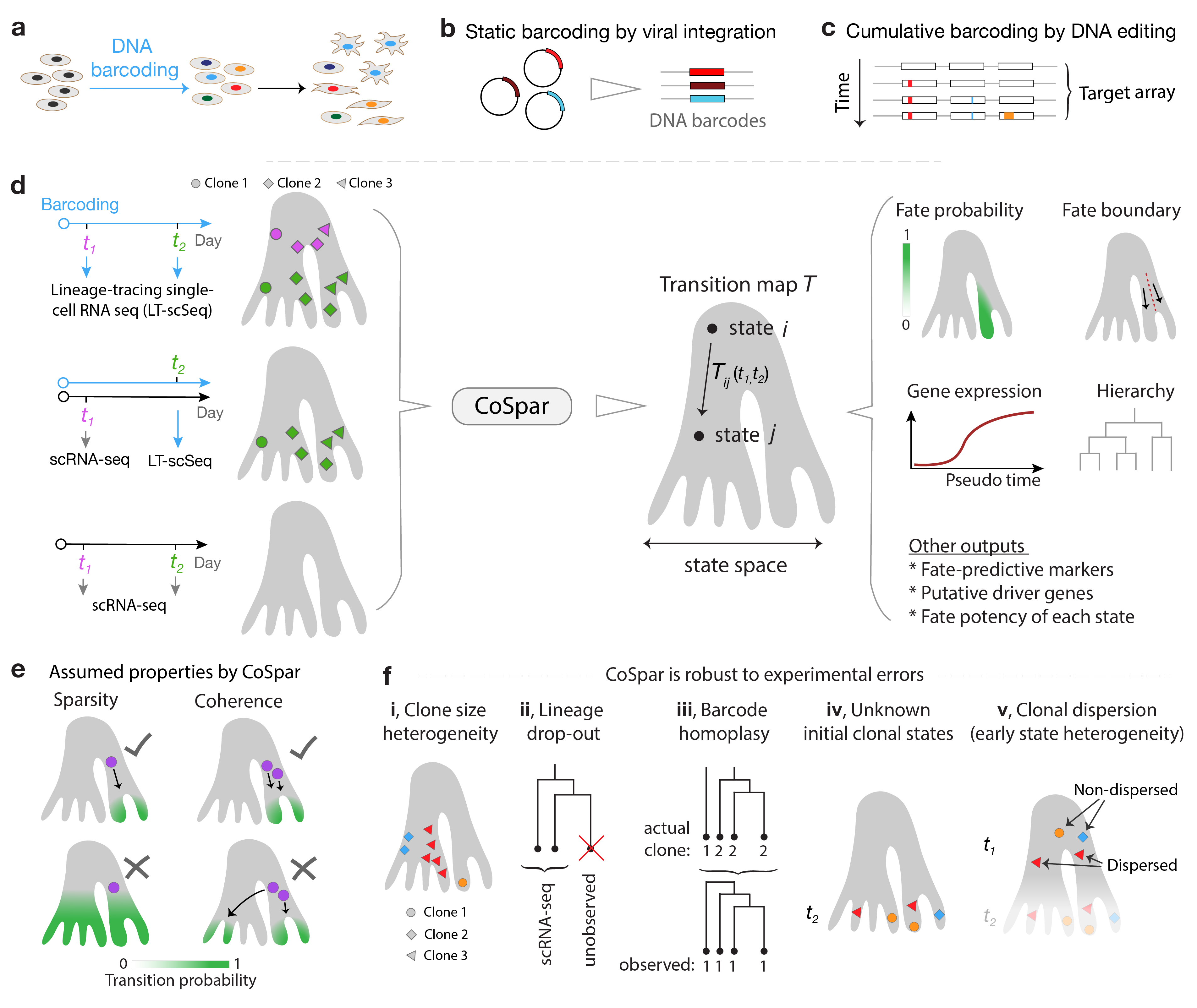
bf6e8a48935647878c0e6c6e135d7134

CoSpar Overview. The transition matrix T computed by maximum likelihood estimation.

</figure>

[1]:

#!pip3 install cospar

[2]:

import cospar as cs
import scanpy as sc
cs.settings.verbosity=2

[3]:

cs.settings.set_figure_params()

Data from Weinreb et al Science 2020.

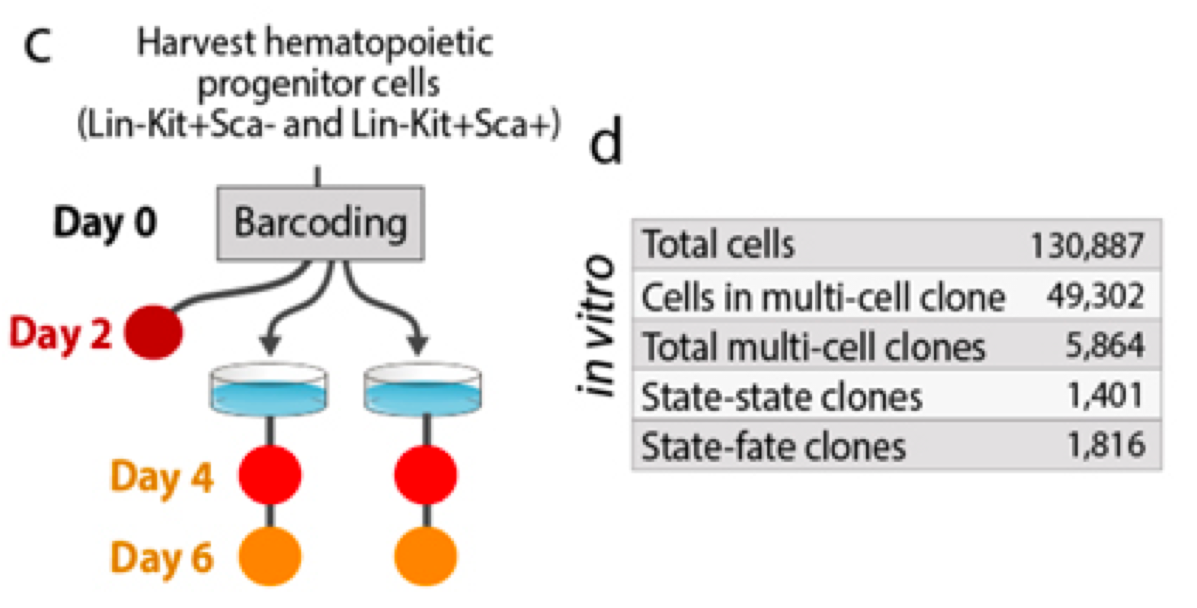
6e3033d21601408e9b755f78d16e7ed7

Data collection strategy.

</figure>

[4]:

adata_orig = sc.read_h5ad("adata_cospar_hspc.h5ad")

Required slots in annData for CoSpar:

  • adata.X: state count matrix, shape (n_cell, n_gene). This should not be log-normalized.

  • adata.var_names: list of gene names, shape (n_genes,).

  • adata.obs[‘time_info’]: time annotation (type: str) for each cell, shape (n_cell,).

  • adata.obs[‘state_info’]: state annotation for each cell, shape (n_cell, 1). [Optional. Can be generated in preprocessing.

  • adata.obsm[‘X_clone’]: clonal labels for each cell in the form of np.array or sparse matrix, shape (n_cell, n_clone).

  • adata.obsm[‘X_pca’]: PCA matrix, shape (n_cell, n_pcs). [Optional. Can be generated in preprocessing.

  • adata.obsm[‘X_emb’]: two-dimensional embedding, shape (n_cell, 2). [Optional. Can be generated in preprocessing.

[5]:

cs.hf.set_up_folders() # NB we did not run this in lecture but will be necessary

[6]:

adata_orig

[6]:

AnnData object with n_obs × n_vars = 7438 × 25289
    obs: 'time_info', 'state_info'
    uns: 'clonal_time_points', 'data_des', 'state_info_colors', 'time_info_colors', 'time_ordering'
    obsm: 'X_clone', 'X_emb', 'X_pca'

[7]:

sc.pl.pca(adata_orig, color='state_info', projection='3d')
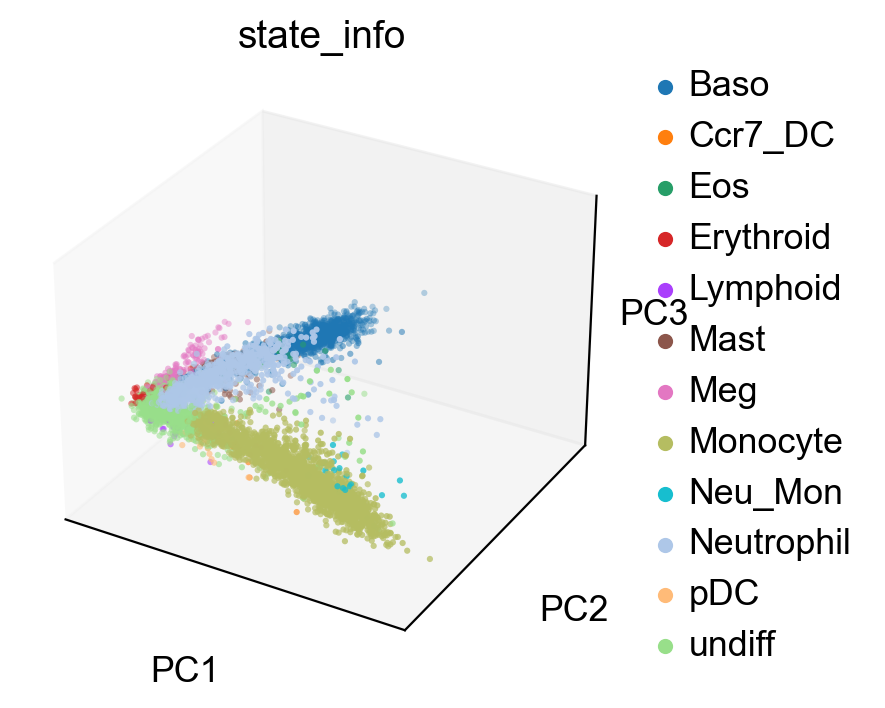
../_images/day_17_Lineage_Tracing_Analysis_9_0.png 
[8]:

sc.pl.embedding(adata_orig, basis="emb",color="state_info")
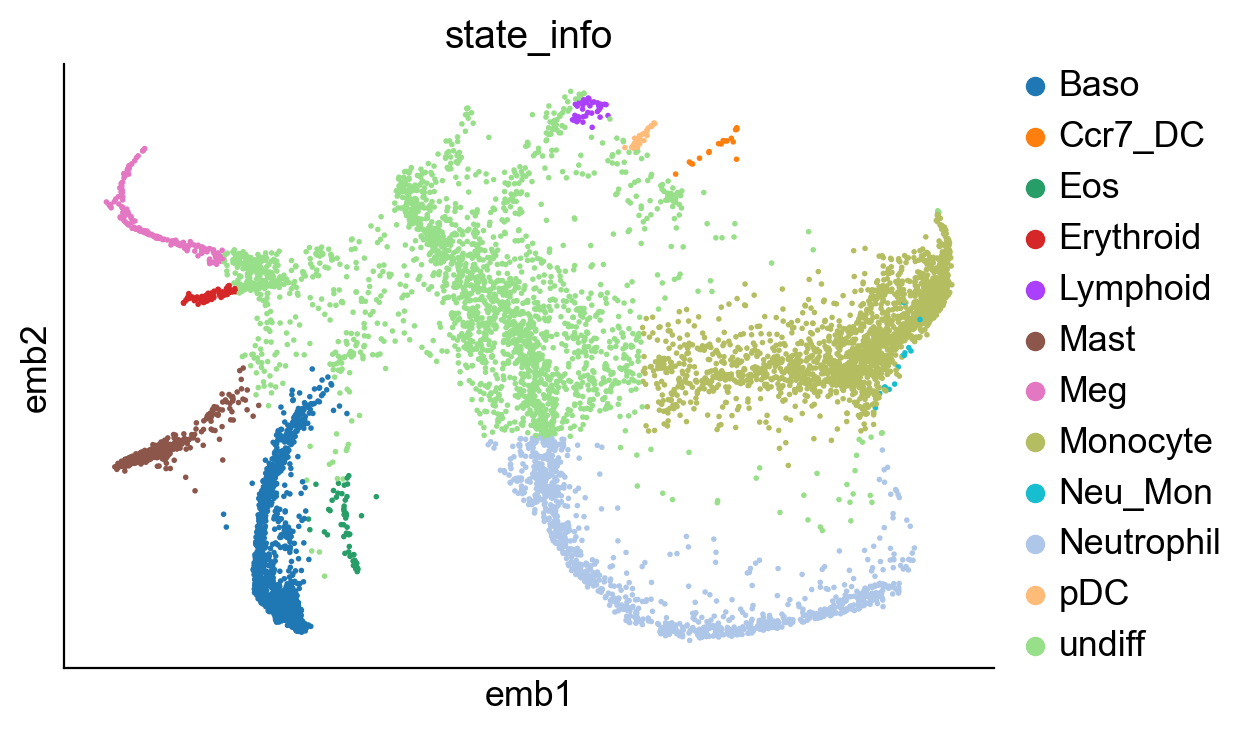
../_images/day_17_Lineage_Tracing_Analysis_10_0.png 
[9]:

sc.pl.embedding(adata_orig, basis="emb",color=['Ccr7'])
../_images/day_17_Lineage_Tracing_Analysis_11_0.png 
[10]:

sc.pl.embedding(adata_orig, basis="emb",color=['time_info'])
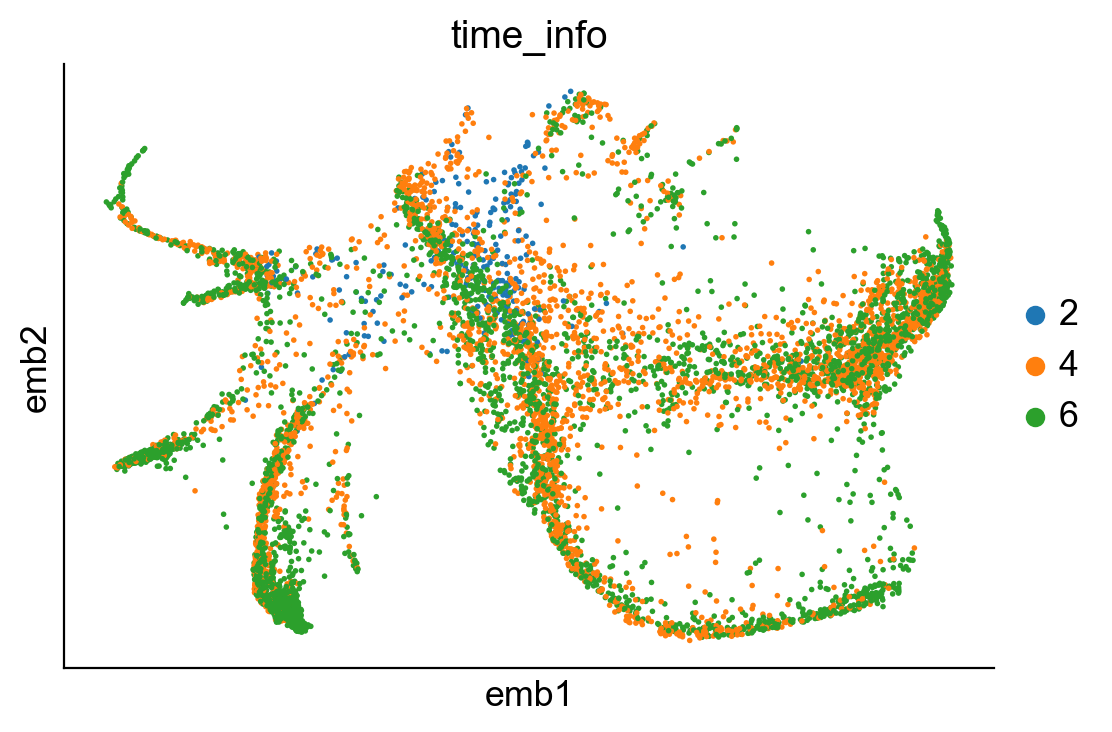
../_images/day_17_Lineage_Tracing_Analysis_12_0.png

We can examine the location of clones on embeddings

[11]:

cs.pl.clones_on_manifold(adata_orig,selected_clone_list=[151],color_list=['black','red','blue'])
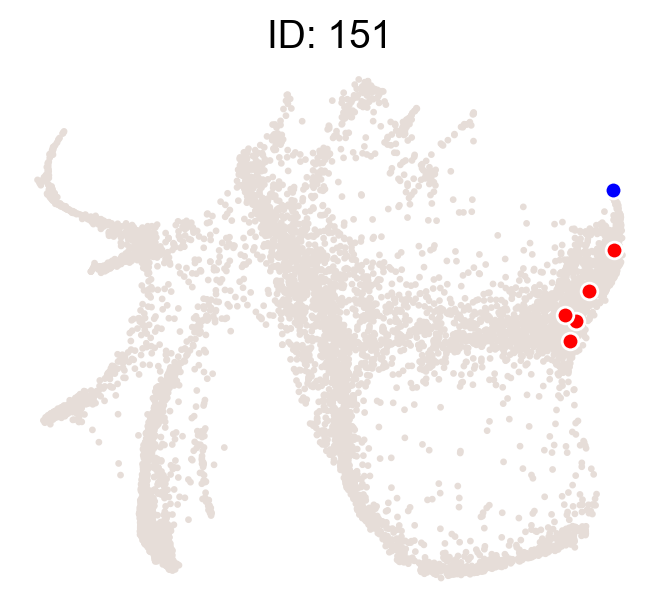
../_images/day_17_Lineage_Tracing_Analysis_14_0.png 
[12]:

cs.pl.clones_on_manifold(adata_orig,selected_clone_list=[200],color_list=['black','red','blue'])
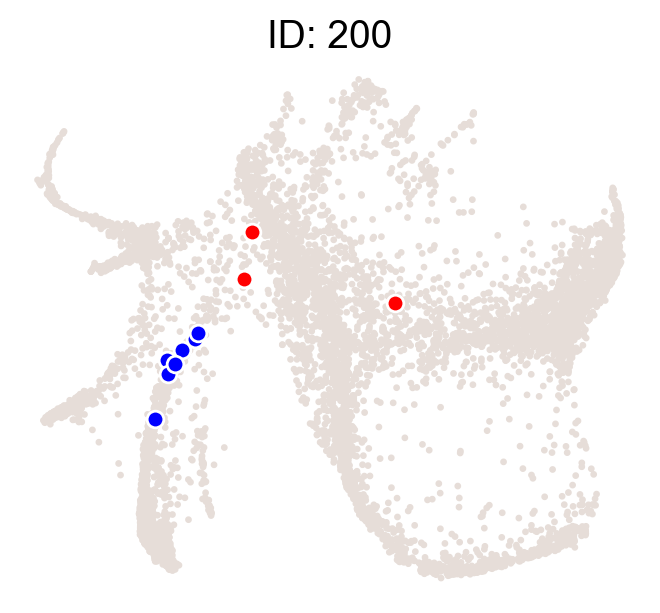
../_images/day_17_Lineage_Tracing_Analysis_15_0.png 
[13]:

cs.pl.clones_on_manifold(adata_orig,selected_clone_list=[0],color_list=['black','red','blue'])
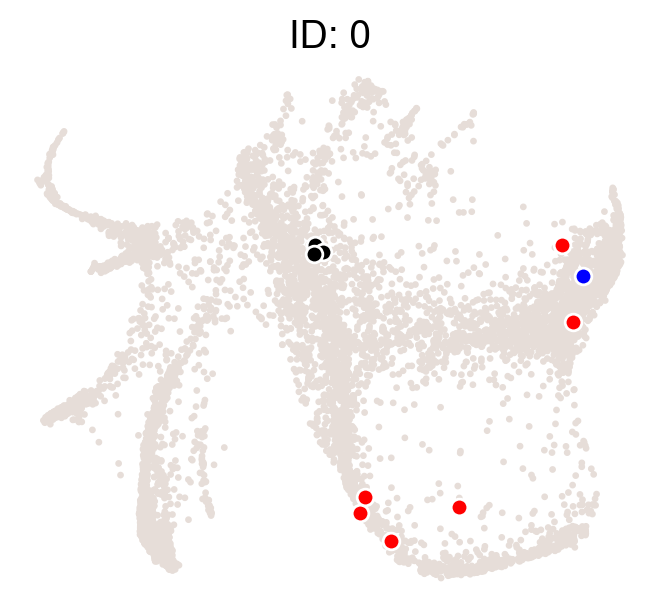
../_images/day_17_Lineage_Tracing_Analysis_16_0.png

How often are clones shared across cell types? This analysis done for given time point

[14]:

selected_times='4'
selected_fates=['Ccr7_DC','Mast','Meg','pDC','Eos','Lymphoid','Erythroid','Baso',  'Neutrophil', 'Monocyte']
cs.tl.fate_coupling(adata_orig,source='X_clone',selected_fates=selected_fates,selected_times=selected_times)
cs.pl.fate_coupling(adata_orig,source='X_clone')

Results saved as dictionary at adata.uns['fate_coupling_X_clone']

[14]:

<AxesSubplot:title={'center':'source: X_clone'}>
../_images/day_17_Lineage_Tracing_Analysis_18_2.png 
[15]:

selected_times='6'
selected_fates=['Ccr7_DC','Mast','Meg','pDC','Eos','Lymphoid','Erythroid','Baso',  'Neutrophil', 'Monocyte']
cs.tl.fate_coupling(adata_orig,source='X_clone',selected_fates=selected_fates,selected_times=selected_times)
cs.pl.fate_coupling(adata_orig,source='X_clone')

Results saved as dictionary at adata.uns['fate_coupling_X_clone']

[15]:

<AxesSubplot:title={'center':'source: X_clone'}>
../_images/day_17_Lineage_Tracing_Analysis_19_2.png

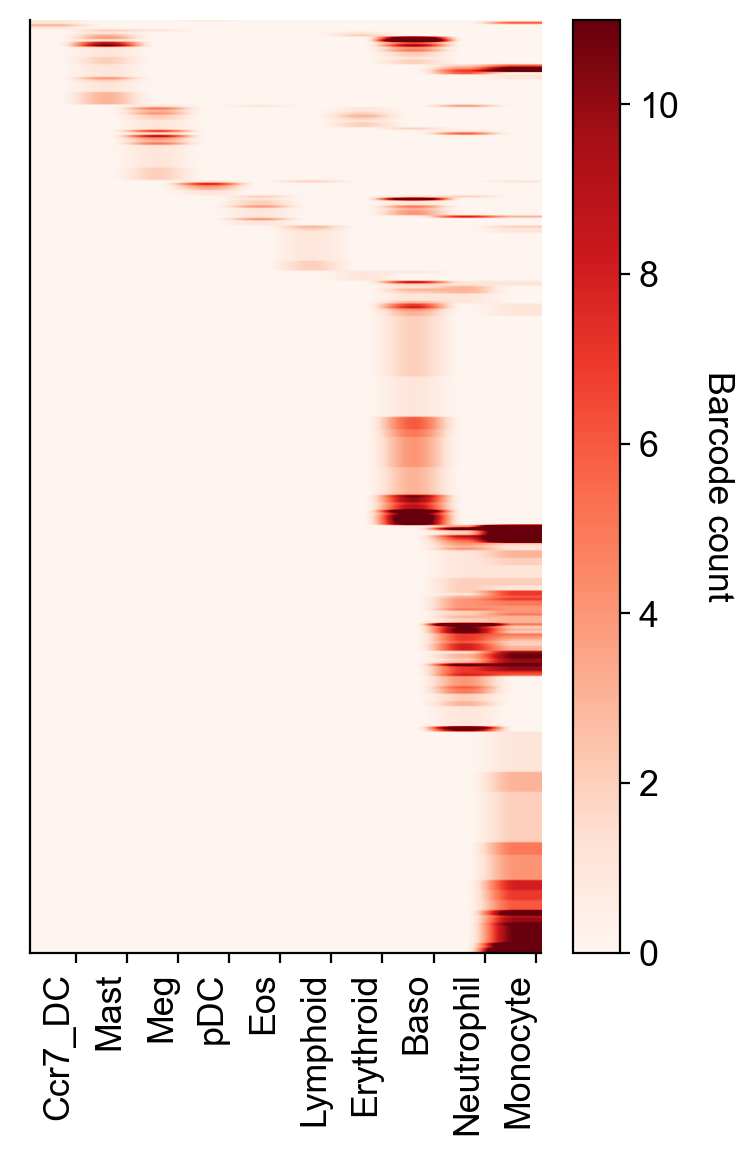
We can look at barcode distributions across cell types, too

[16]:

selected_times='4'
selected_fates=['Ccr7_DC','Mast','Meg','pDC','Eos','Lymphoid','Erythroid','Baso',  'Neutrophil', 'Monocyte']
cs.pl.barcode_heatmap(adata_orig,selected_times=selected_times, selected_fates=selected_fates, color_bar=True)

Data saved at adata.uns['barcode_heatmap']

[16]:

<AxesSubplot:>
../_images/day_17_Lineage_Tracing_Analysis_21_2.png 
[17]:

adata=cs.tmap.infer_Tmap_from_multitime_clones(adata_orig,clonal_time_points=['2','4','6'],later_time_point='6',
        smooth_array=[20,15,10],sparsity_threshold=0.2,max_iter_N=3)

Trying to set attribute `._uns` of view, copying.

------Compute the full Similarity matrix if necessary------
------Infer transition map between initial time points and the later time one------
--------Current initial time point: 2--------
Step 1: Select time points
Number of multi-time clones post selection: 185
Step 2: Optimize the transition map recursively
Load pre-computed similarity matrix
Iteration 1, Use smooth_round=20
Iteration 2, Use smooth_round=15
Iteration 3, Use smooth_round=10
Convergence (CoSpar, iter_N=3): corr(previous_T, current_T)=0.953
--------Current initial time point: 4--------
Step 1: Select time points
Number of multi-time clones post selection: 500
Step 2: Optimize the transition map recursively
Load pre-computed similarity matrix
Iteration 1, Use smooth_round=20
Iteration 2, Use smooth_round=15
Iteration 3, Use smooth_round=10
Convergence (CoSpar, iter_N=3): corr(previous_T, current_T)=0.974
-----------Total used time: 17.448920965194702 s ------------

[18]:

adata

[18]:

AnnData object with n_obs × n_vars = 7438 × 25289
    obs: 'time_info', 'state_info'
    uns: 'clonal_time_points', 'data_des', 'state_info_colors', 'time_info_colors', 'time_ordering', 'available_map', 'fate_coupling_X_clone', 'barcode_heatmap', 'Tmap_cell_id_t1', 'Tmap_cell_id_t2', 'clonal_cell_id_t1', 'clonal_cell_id_t2', 'sp_idx', 'transition_map', 'intraclone_transition_map'
    obsm: 'X_clone', 'X_emb', 'X_pca'

[19]:

adata.uns['transition_map'].shape

[19]:

(3392, 4046)

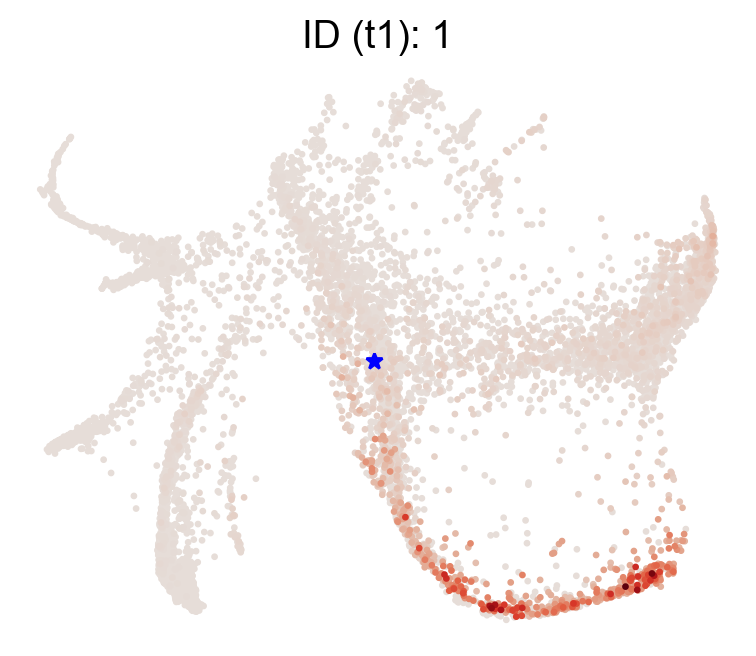
Now, given an state, we can examine it’s likely trajectory using the transition matrix just computed

[20]:

selected_state_id_list=[1]

cs.pl.single_cell_transition(adata,selected_state_id_list=selected_state_id_list, color_bar=False,
                                    source='transition_map',map_backward=False)
../_images/day_17_Lineage_Tracing_Analysis_26_0.png 
[21]:

selected_state_id_list=[100]

cs.pl.single_cell_transition(adata,selected_state_id_list=selected_state_id_list, color_bar=False,
                                    source='transition_map',map_backward=False)
../_images/day_17_Lineage_Tracing_Analysis_27_0.png

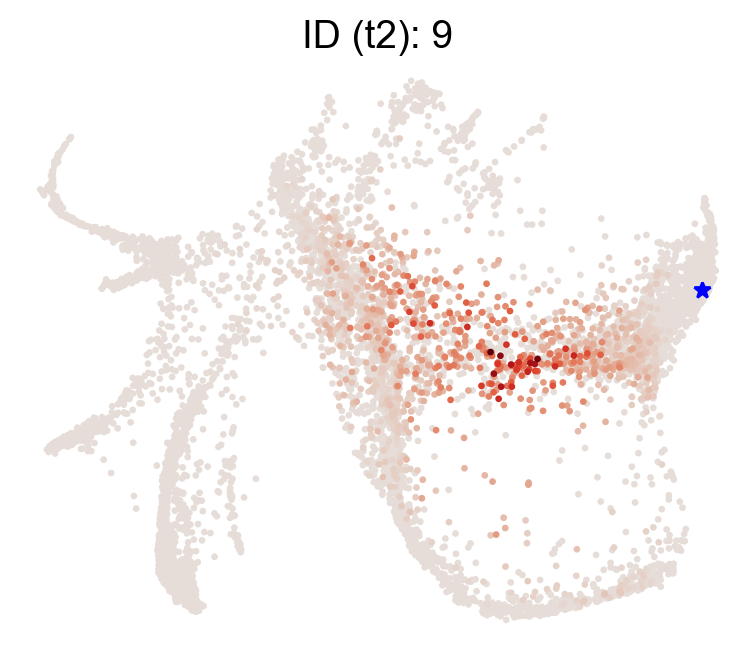
Similarly, we can compute transition profiles for end states (where did they originate)?

[22]:

selected_state_id_list=[9]
cs.pl.single_cell_transition(adata,selected_state_id_list=selected_state_id_list, color_bar=False,
                                    source='transition_map',map_backward=True)
../_images/day_17_Lineage_Tracing_Analysis_29_0.png

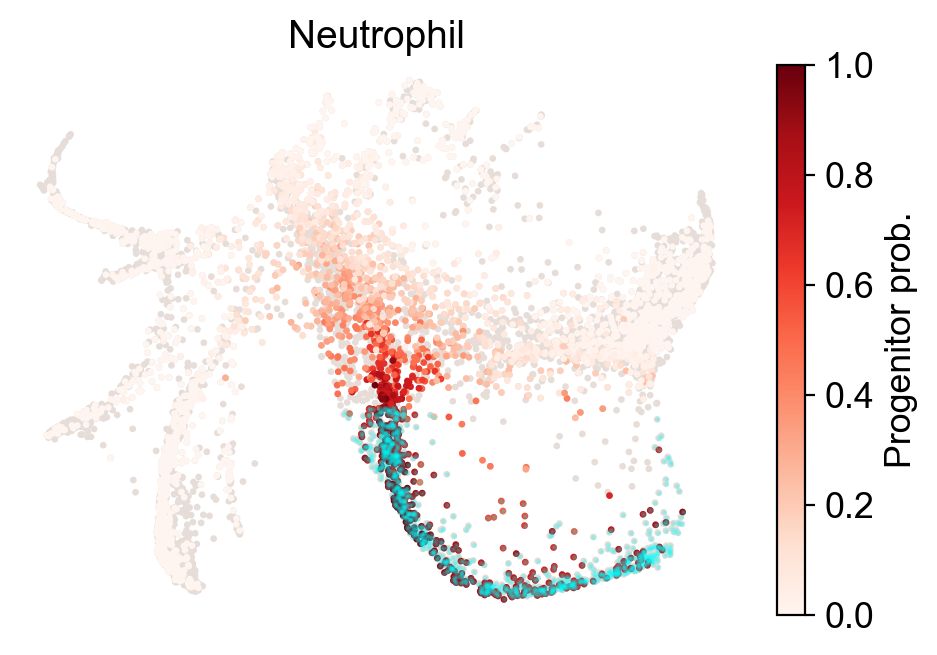
Now let’s examine a fate map. Given a cluster/state/end-point, where did it originate?

[23]:

cs.tl.fate_map(adata,selected_fates=['Neutrophil','Monocyte'],
               source='transition_map',map_backward=True)
cs.pl.fate_map(adata,selected_fates=['Neutrophil'],
               source='transition_map',plot_target_state=True,show_histogram=False)

Results saved at adata.obs['fate_map_transition_map_Neutrophil']
Results saved at adata.obs['fate_map_transition_map_Monocyte']
../_images/day_17_Lineage_Tracing_Analysis_31_1.png 
[24]:

cs.pl.fate_map(adata,selected_fates=['Monocyte'],
               source='transition_map',plot_target_state=True,show_histogram=False)
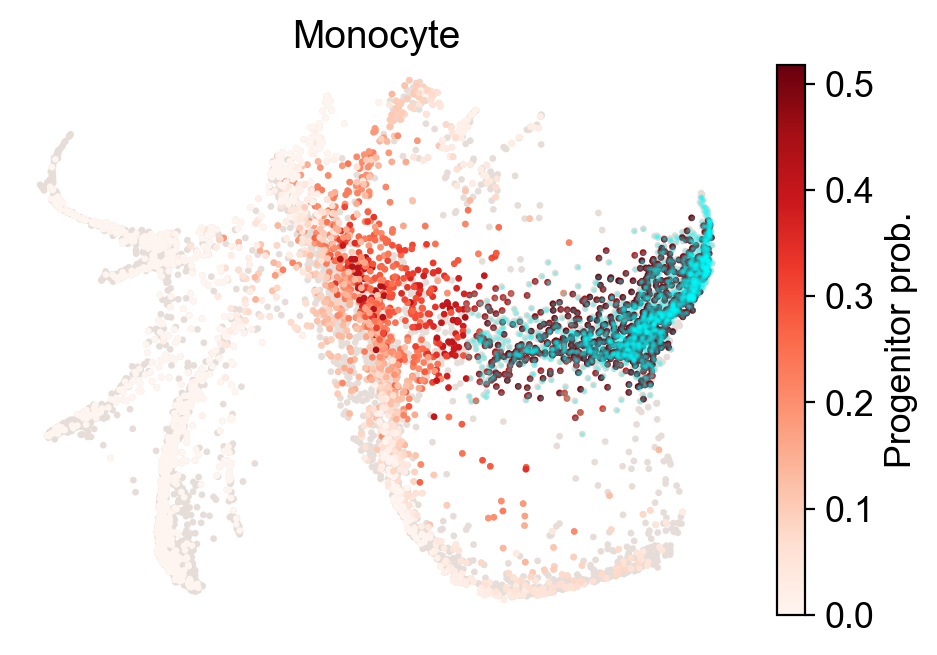
../_images/day_17_Lineage_Tracing_Analysis_32_0.png

Compute fate potency as the normalized sum of potential endpoints

[25]:

cs.tl.fate_potency(adata,source='transition_map',
            map_backward=True,method='norm-sum',fate_count=True)
cs.pl.fate_potency(adata,source='transition_map')

Results saved at adata.obs['fate_map_transition_map_Mast']
Results saved at adata.obs['fate_map_transition_map_Erythroid']
Results saved at adata.obs['fate_map_transition_map_Ccr7_DC']
Results saved at adata.obs['fate_map_transition_map_Eos']
Results saved at adata.obs['fate_map_transition_map_Lymphoid']
Results saved at adata.obs['fate_map_transition_map_pDC']
Results saved at adata.obs['fate_map_transition_map_undiff']
Results saved at adata.obs['fate_map_transition_map_Baso']
Results saved at adata.obs['fate_map_transition_map_Monocyte']
Results saved at adata.obs['fate_map_transition_map_Neu_Mon']
Results saved at adata.obs['fate_map_transition_map_Meg']
Results saved at adata.obs['fate_map_transition_map_Neutrophil']
Results saved at adata.obs['fate_potency_transition_map']
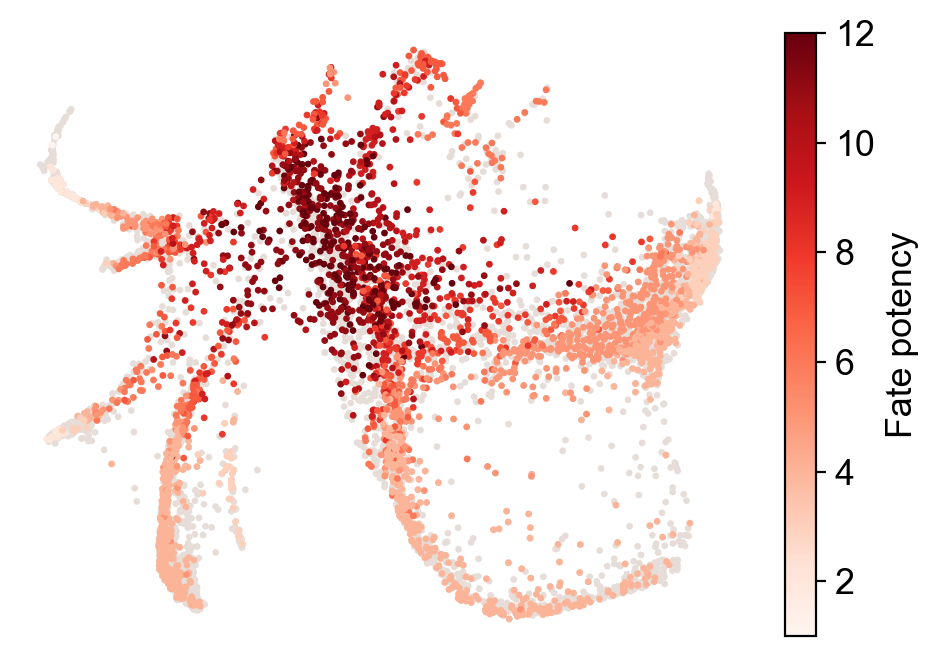
../_images/day_17_Lineage_Tracing_Analysis_34_1.png

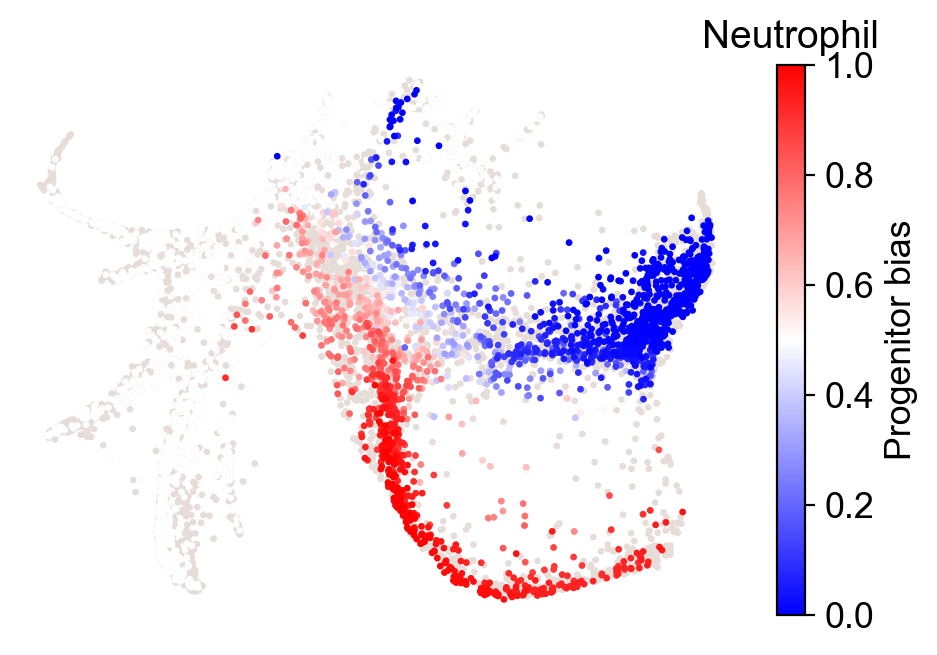
Now let’s examine fate bias between two cell types/states/endpoints a and b. Computed as Pr(endstate = a) / Pr(endstate=a) + Pr(endstate=b)

[26]:

cs.tl.fate_bias(adata,selected_fates=['Neutrophil','Monocyte'],source='transition_map',pseudo_count=0,sum_fate_prob_thresh=0.1)
cs.pl.fate_bias(adata,selected_fates=['Neutrophil','Monocyte'],source='transition_map',plot_target_state=False,selected_times=['4'])

Results saved at adata.obs['fate_map_transition_map_Neutrophil']
Results saved at adata.obs['fate_map_transition_map_Monocyte']
Results saved at adata.obs['fate_bias_transition_map_Neutrophil*Monocyte']
../_images/day_17_Lineage_Tracing_Analysis_36_1.png

Fate coupling from transition matrix

[27]:

selected_fates=['Ccr7_DC','Mast','Meg','pDC','Eos','Lymphoid','Erythroid','Baso',  'Neutrophil', 'Monocyte']
cs.tl.fate_coupling(adata,selected_fates=selected_fates,source='transition_map')
cs.pl.fate_coupling(adata,source='transition_map')

Results saved as dictionary at adata.uns['fate_coupling_transition_map']

[27]:

<AxesSubplot:title={'center':'source: transition_map'}>
../_images/day_17_Lineage_Tracing_Analysis_38_2.png 
[28]:

# compared to from clonal data alone
cs.tl.fate_coupling(adata,selected_fates=selected_fates,source='X_clone')
cs.pl.fate_coupling(adata,source='X_clone')

Results saved as dictionary at adata.uns['fate_coupling_X_clone']

[28]:

<AxesSubplot:title={'center':'source: X_clone'}>
../_images/day_17_Lineage_Tracing_Analysis_39_2.png

Now reconstruct the hierarchy

[29]:

cs.tl.fate_hierarchy(adata,selected_fates=selected_fates,source='transition_map')
cs.pl.fate_hierarchy(adata,source='transition_map')

Results saved as dictionary at adata.uns['fate_hierarchy_transition_map']

            /-Baso
         /-|
      /-|   \-Eos
     |  |
   /-|   \-Mast
  |  |
  |  |   /-Erythroid
  |   \-|
--|      \-Meg
  |
  |      /-Monocyte
  |   /-|
  |  |   \-Neutrophil
   \-|
     |      /-pDC
     |   /-|
      \-|   \-Ccr7_DC
        |
         \-Lymphoid

What distinguishes progenitors likely to become monocytes from those that are likely to become neutrophils?

[30]:

import numpy as np

cs.tl.progenitor(adata, selected_fates=['Neutrophil','Monocyte'],
 source='transition_map', map_backward=True,
    bias_threshold_A=0.5,bias_threshold_B=0.5, sum_fate_prob_thresh=0.2, avoid_target_states=True)
cs.pl.progenitor(adata, selected_fates=['Neutrophil','Monocyte'],
 source='transition_map')

Results saved at adata.obs['fate_map_transition_map_Neutrophil']
Results saved at adata.obs['fate_map_transition_map_Monocyte']
Results saved at adata.obs['fate_bias_transition_map_Neutrophil*Monocyte']
Results saved at adata.obs[f'progenitor_transition_map_Neutrophil'] and adata.obs[f'diff_trajectory_transition_map_Neutrophil']
Results saved at adata.obs[f'progenitor_transition_map_Monocyte'] and adata.obs[f'diff_trajectory_transition_map_Monocyte']
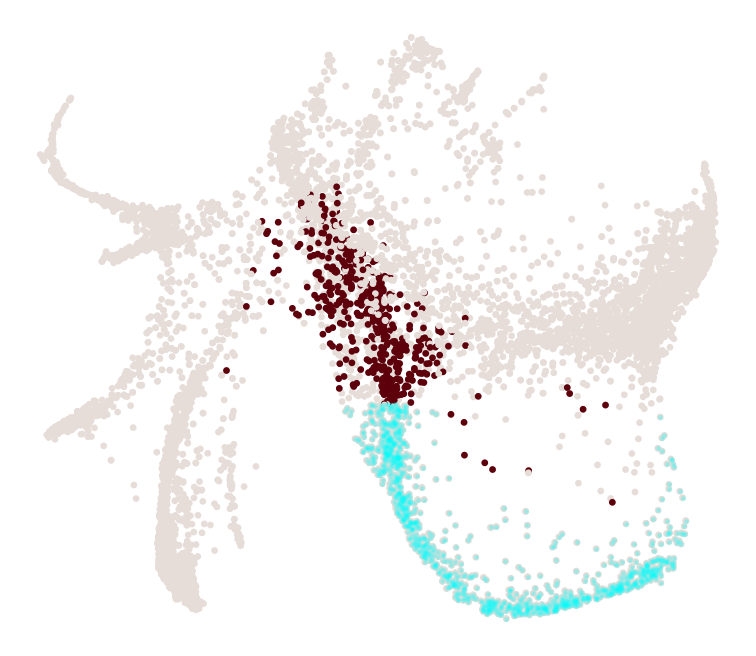
../_images/day_17_Lineage_Tracing_Analysis_43_1.png
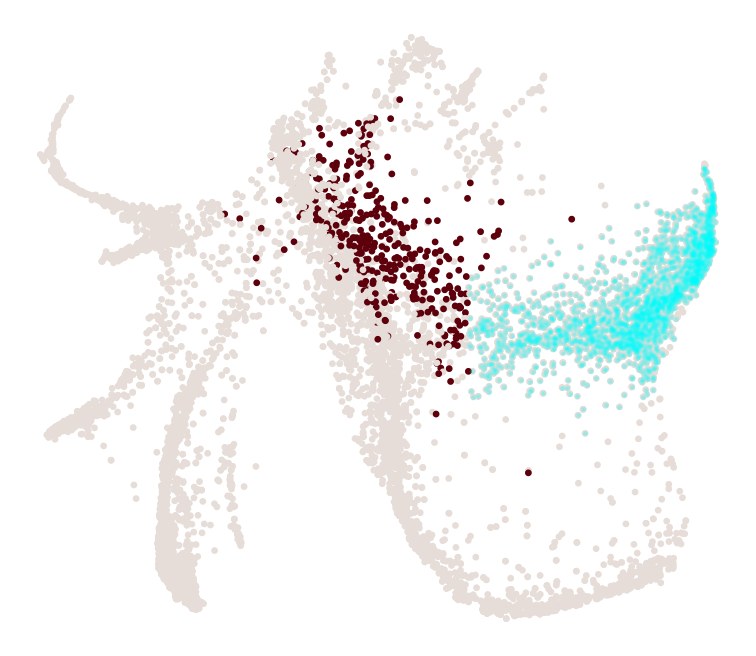
../_images/day_17_Lineage_Tracing_Analysis_43_2.png

note that resuls are stored as follows:

adata.obs[f'progenitor_{source}_{fate_name}']

adata.obs[f'diff_trajectory_{source}_{fate_name}']

[31]:


cell_group_A=np.array(adata.obs['diff_trajectory_transition_map_Neutrophil'])
cell_group_B=np.array(adata.obs['diff_trajectory_transition_map_Monocyte'])
dge_gene_A, dge_gene_B=cs.tl.differential_genes(adata,cell_group_A=cell_group_A,cell_group_B=cell_group_B,FDR_cutoff=0.05)

[32]:

dge_gene_A

[32]:
index gene Qvalue mean_1 mean_2 ratio
0 5 Mmp8 0.000000e+00 0.563468 11.657158 -3.017132
1 1 Wfdc17 0.000000e+00 0.078693 7.124163 -2.912935
2 9 Lpl 2.733934e-267 0.240403 8.100443 -2.875127
3 10 Fabp5 1.209024e-246 1.652049 15.526230 -2.639579
4 3 Psap 0.000000e+00 1.660915 14.049889 -2.499758
... ... ... ... ... ... ...
1067 2060 H3f3a 7.928128e-04 4.989668 5.169685 -0.042721
1068 3290 AB124611 4.108763e-02 0.605892 0.648909 -0.038136
1069 3124 Tmpo 3.081903e-02 0.922378 0.929656 -0.005451
1070 2697 Ffar2 1.080521e-02 0.608486 0.609789 -0.001169
1071 2857 Nom1 1.716971e-02 0.235725 0.236709 -0.001149

1072 rows × 6 columns

[33]:

dge_gene_B

[33]:
index gene Qvalue mean_1 mean_2 ratio
0 36 Ngp 5.649159e-144 54.840271 0.418010 5.299366
1 33 S100a9 1.356053e-148 80.231552 8.239202 3.136200
2 38 S100a8 1.789692e-139 48.096233 8.031301 2.442606
3 21 Elane 8.662786e-184 8.812663 1.012724 2.285495
4 222 Camp 2.724041e-46 4.027065 0.032162 2.284047
... ... ... ... ... ... ...
2320 3044 Tex261 2.636864e-02 0.307811 0.299247 0.009477
2321 3154 Ndufs4 3.271385e-02 0.158712 0.151988 0.008397
2322 2164 Bub1b 1.311236e-03 0.291533 0.285507 0.006747
2323 3128 Socs2 3.108334e-02 0.247205 0.242337 0.005642
2324 3392 Trpm7 4.928712e-02 0.231395 0.227887 0.004117

2325 rows × 6 columns

[34]:

sc.pl.embedding(adata, basis="emb",color=['Mmp8', 'Ngp'])
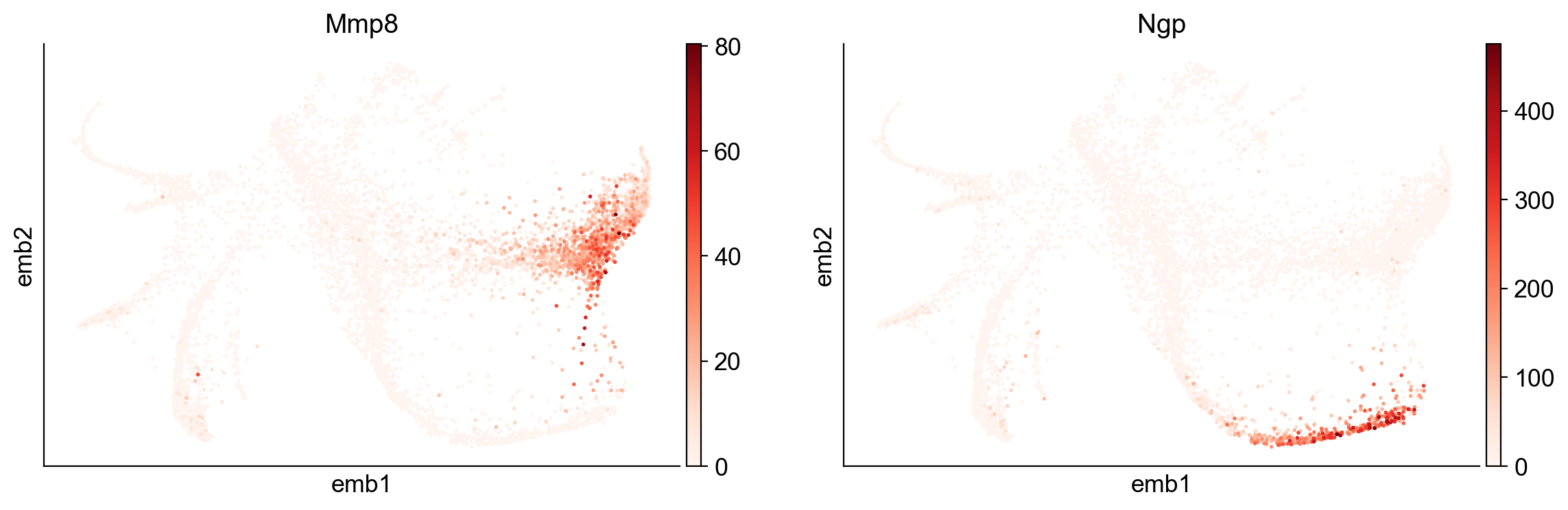
../_images/day_17_Lineage_Tracing_Analysis_48_0.png 
[35]:

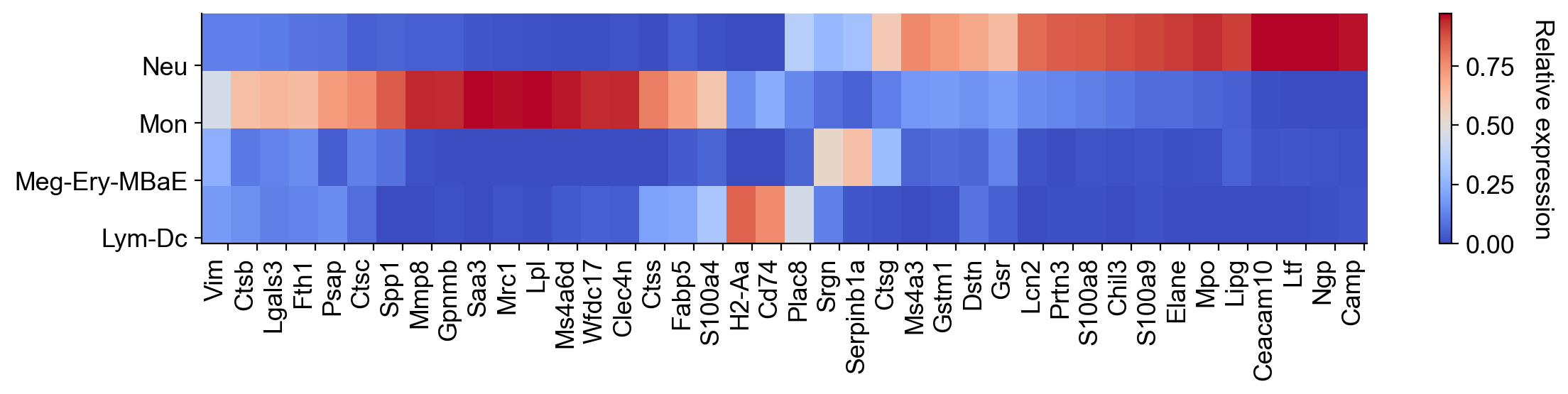
gene_list=list(dge_gene_A['gene'][:20])+list(dge_gene_B['gene'][:20]) #select the top 20 genes from both populations

selected_fates=['Neutrophil','Monocyte',['Baso','Eos','Erythroid','Mast','Meg'],['pDC','Ccr7_DC','Lymphoid']]
renames=['Neu','Mon','Meg-Ery-MBaE','Lym-Dc']
gene_expression_matrix=cs.pl.gene_expression_heatmap(adata,selected_genes=gene_list,selected_fates=selected_fates,
                            rename_fates=renames,fig_width=12)
../_images/day_17_Lineage_Tracing_Analysis_49_0.png

To identify undifferentiated cells that are biased towards either of these lineages, do the following:

[36]:


cell_group_A=np.array(adata.obs['progenitor_transition_map_Neutrophil'])
cell_group_B=np.array(adata.obs['progenitor_transition_map_Monocyte'])

Perform differential gene expression analysis between these two groups of undiff cells. You may need to adjust FDR_cutoff.

[37]:

dge_gene_A, dge_gene_B=cs.tl.differential_genes(adata,cell_group_A=cell_group_A,cell_group_B=cell_group_B,FDR_cutoff=0.05)

[38]:

dge_gene_A

[38]:
index gene Qvalue mean_1 mean_2 ratio
0 16 Ly6a 9.039739e-11 0.304916 1.487901 -0.930972
1 113 Cd74 8.016464e-04 0.049357 0.590306 -0.599799
2 265 Lpl 1.855205e-02 0.514680 1.288570 -0.595433
3 15 Ifi203 3.450286e-11 0.263296 0.855959 -0.554973
4 129 Ctsc 1.435103e-03 1.143432 2.044259 -0.506169
... ... ... ... ... ... ...
83 241 Nrros 1.383268e-02 1.127532 1.403783 -0.176126
84 115 Rps23 8.607369e-04 11.237831 12.805717 -0.173918
85 221 Rpl7 1.126278e-02 6.221563 6.941932 -0.137179
86 264 mt-Nd1 1.835382e-02 33.804676 36.876221 -0.122011
87 314 Rpl4 3.784367e-02 8.111238 8.714950 -0.092559

88 rows × 6 columns

[39]:

dge_gene_B

[39]:
index gene Qvalue mean_1 mean_2 ratio
0 61 S100a9 3.328465e-05 2.505955 0.577988 1.151722
1 46 S100a8 3.593216e-06 2.456529 0.629346 1.085031
2 3 Elane 8.796332e-27 5.110261 1.924245 1.063170
3 1 Gstm1 5.398384e-28 3.022064 0.980477 1.022088
4 2 Mpo 9.856078e-28 2.592695 0.801986 0.995479
... ... ... ... ... ... ...
249 266 Hdlbp 1.902594e-02 0.445726 0.342975 0.106362
250 318 Adrbk1 3.892046e-02 0.552127 0.445955 0.102224
251 339 Cebpa 4.920242e-02 0.292482 0.204556 0.101643
252 270 Canx 1.991304e-02 0.748365 0.635935 0.095892
253 329 Pcgf5 4.420974e-02 0.150279 0.077339 0.094511

254 rows × 6 columns

[40]:

sc.pl.embedding(adata, basis="emb",color=['Ly6a', 'S100a9'])
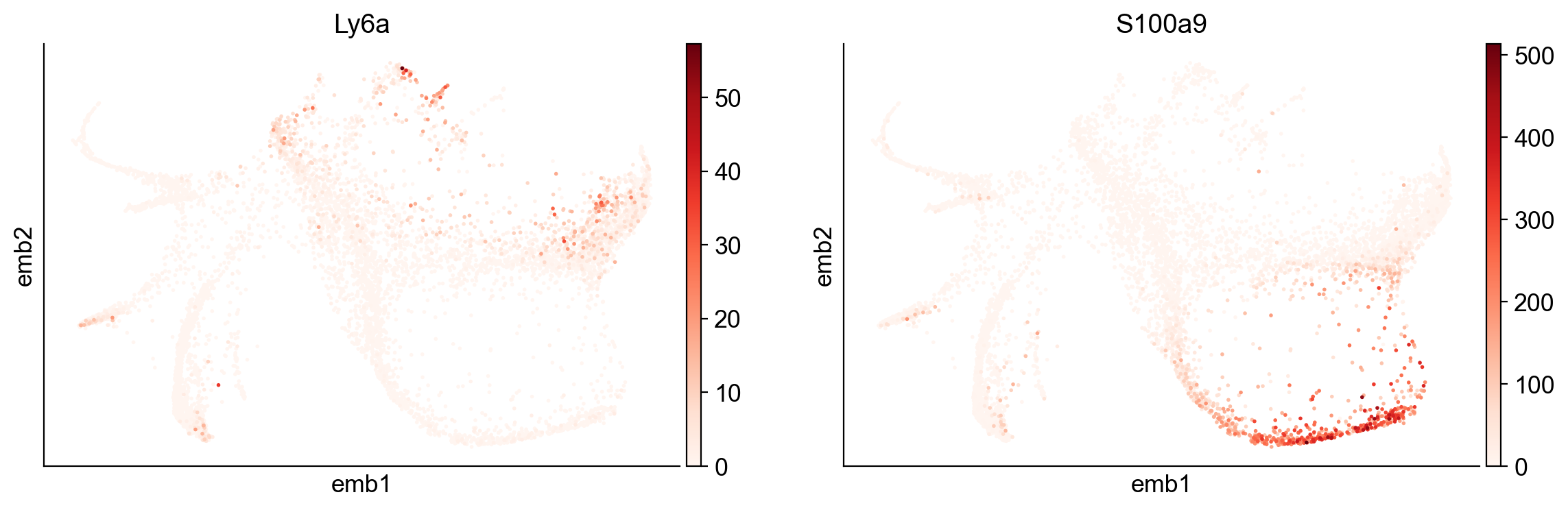
../_images/day_17_Lineage_Tracing_Analysis_56_0.png

Here is a summary of the functions:

e2bc3dae77fb45748b6b657c94222038

CoSpar function summary.

</figure>